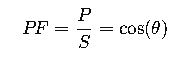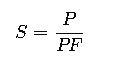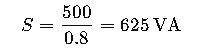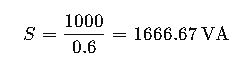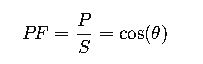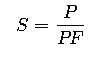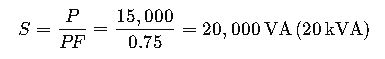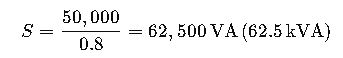In electrical engineering, converting real power (watts, W) to apparent power (VA) ensures accurate system analysis. This conversion depends on the power factor (PF), a number between 0 and 1 representing phase difference.
Watts / VA → Power Factor Calculator
What is Power Factor?
Formula used
Power Factor (PF) and Its Significance
The power factor is defined as the ratio of real power (P) to apparent power (S):
Where:
- P is the real power in watts (W),
- S is the apparent power in volt-amperes (VA),
- θ is the phase angle between the voltage and current waveforms.
A power factor of 1 (or 100%) indicates that all the energy supplied by the source is being used effectively for work, typical of purely resistive loads. A lower power factor signifies that some energy is wasted, often due to inductive or capacitive components in the load.
Conversion Formula: Watts to VA
To convert real power (watts) to apparent power (volt-amperes), the following formula is used:
Where:
- S is the apparent power in VA,
- P is the real power in W,
- PF is the power factor.
This formula is applicable to AC circuits, where the voltage and current are not perfectly in phase.
Common Power Factor Values
The power factor varies depending on the type of equipment and its load characteristics:
| Equipment Type | Typical Power Factor (PF) |
|---|---|
| Resistive loads (e.g., heaters) | 1.0 (unity) |
| Incandescent lighting | 1.0 |
| Fluorescent lighting | 0.9–0.95 |
| Inductive loads (e.g., motors) | 0.7–0.9 |
| Capacitive loads | 0.9–1.0 |
| Uninterruptible Power Supplies (UPS) | 0.6–0.8 |
These values are indicative and can vary based on specific operating conditions and equipment quality.
Practical Examples
Example 1: Calculating VA for a 500 W Load with PF of 0.8
Given:
- Real power P=500 W
- Power factor PF=0.8
Using the formula:
This means the apparent power required is 625 VA.
Example 2: Determining VA for a 1000 W Load with PF of 0.6
Given:
- Real power P=1000 W
- Power factor PF=0.6
Using the formula:
Here, the apparent power required is approximately 1666.67 VA.
Importance of Correct Power Factor in System Design
Accurate calculation of VA is crucial for:
- Sizing electrical components: Ensuring transformers, generators, and UPS systems are appropriately rated.
- Energy efficiency: Identifying and mitigating low power factor conditions to reduce energy losses.
- Compliance: Adhering to standards and regulations that may impose limits on allowable power factor levels.
Power Factor and Its Implications on Electrical Systems
Power factor (PF) is a crucial parameter in electrical engineering, representing the efficiency with which electrical power is converted into useful work output. It is defined as the ratio of real power (P) to apparent power (S):
Where:
- P is the real power in watts (W),
- S is the apparent power in volt-amperes (VA),
- θ is the phase angle between the voltage and current waveforms.
A power factor of 1 (or 100%) indicates that all the energy supplied by the source is being used effectively for work, typical of purely resistive loads. A lower power factor signifies that some energy is wasted, often due to inductive or capacitive components in the load.
Conversion Formula: Watts to VA
To convert real power (watts) to apparent power (volt-amperes), the following formula is used:
Where:
- S is the apparent power in VA,
- P is the real power in W,
- PF is the power factor.
This formula is applicable to AC circuits, where the voltage and current are not perfectly in phase.
Common Power Factor Values
The power factor varies depending on the type of equipment and its load characteristics:
| Equipment Type | Typical Power Factor (PF) |
|---|---|
| Resistive loads (e.g., heaters) | 1.0 (unity) |
| Incandescent lighting | 1.0 |
| Fluorescent lighting | 0.9–0.95 |
| Inductive loads (e.g., motors) | 0.7–0.9 |
| Capacitive loads | 0.9–1.0 |
| Uninterruptible Power Supplies (UPS) | 0.6–0.8 |
These values are indicative and can vary based on specific operating conditions and equipment quality.
Example 3: Calculating VA for an Industrial Motor
An industrial motor consumes P=15,000 W with a power factor PF=0.75.
- Interpretation: Even though the motor only uses 15 kW of real power, the electrical system must supply 20 kVA of apparent power to operate properly. This ensures generators and transformers are correctly sized.
Example 4: UPS for a Data Center
A UPS powers servers that consume P=50,000 W with a typical PF of 0.8.
- Interpretation: The UPS must be rated for 62.5 kVA even though the real load is 50 kW. This ensures no overload occurs and the system maintains stability during peak operation.
Improving Power Factor
Maintaining a high power factor reduces losses and improves efficiency. Common methods include:
- Capacitor banks: Compensate for inductive loads like motors and transformers.
- Synchronous condensers: Provide dynamic PF correction in large systems.
- Active power factor correction devices: Used in electronics-heavy installations.
Industry-Specific Power Factor Guidelines
| Industry | Typical PF Range | Notes |
|---|---|---|
| Industrial manufacturing | 0.7 – 0.95 | Motors and heavy machinery |
| Commercial buildings | 0.85 – 0.95 | HVAC and lighting dominate |
| Data centers | 0.9 – 0.99 | Mostly electronic loads |
| Utilities & grid transmission | 0.95 – 1.0 | Reactive power minimization |
Maintaining the PF close to 1 reduces stress on the electrical network and improves energy billing efficiency.
Importance of Correct Power Factor in System Design
Accurate calculation of VA is crucial for:
- Sizing electrical components: Ensuring transformers, generators, and UPS systems are appropriately rated.
- Energy efficiency: Identifying and mitigating low power factor conditions to reduce energy losses.
- Compliance: Adhering to standards and regulations that may impose limits on allowable power factor levels.
Conclusion
Understanding the relationship between watts, volt-amperes, and power factor is fundamental in electrical engineering. Properly converting between these units ensures efficient system design, optimal equipment sizing, and compliance with industry standards. Always consider the specific power factor of your load to make accurate calculations and informed decisions in your electrical projects.