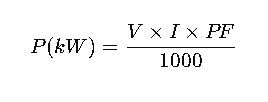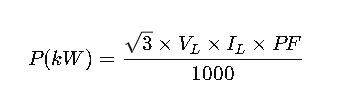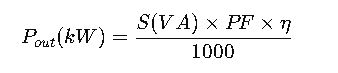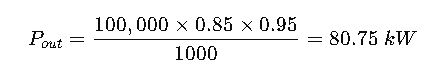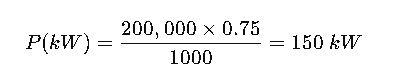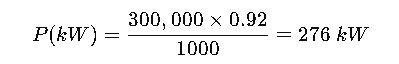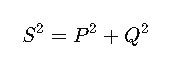The conversion from Volt-Amperes (VA) to Kilowatts (kW) is crucial in electrical engineering. It is essential for designing, sizing, and optimizing systems, offering tables, formulas, and practical examples.
VA ↔ kW Calculator
What PF to use if unknown?
Which voltage to choose?
Formulas used
kW = VA × PF. VA = kW / PF.
Conversion Formula: VA to kW
The core formula for converting VA to kW is:
P(kW) = S(VA) × PF / 1000
Where:
- P(kW) = Real power in kilowatts
- S(VA) = Apparent power in volt-amperes
- PF = Power factor (dimensionless)
This formula is applicable to both single-phase and three-phase AC circuits, with the power factor accounting for the phase difference between voltage and current.
Conversion Tables: Common VA to kW Values
Below are detailed tables illustrating the conversion of VA to kW across various power factors, aiding in quick reference for engineers and technicians.
Single-Phase AC Circuits
| Apparent Power (VA) | Power Factor (PF) | Real Power (kW) |
|---|---|---|
| 1,000 | 0.8 | 0.8 |
| 2,000 | 0.8 | 1.6 |
| 5,000 | 0.8 | 4.0 |
| 10,000 | 0.8 | 8.0 |
| 20,000 | 0.8 | 16.0 |
| 50,000 | 0.8 | 40.0 |
| 100,000 | 0.8 | 80.0 |
| 1,000,000 | 0.8 | 800.0 |
Note: For a power factor of 1.0, the real power equals the apparent power divided by 1,000.
Three-Phase AC Circuits
| Apparent Power (VA) | Power Factor (PF) | Real Power (kW) |
|---|---|---|
| 1,000 | 0.8 | 0.8 |
| 2,000 | 0.8 | 1.6 |
| 5,000 | 0.8 | 4.0 |
| 10,000 | 0.8 | 8.0 |
| 20,000 | 0.8 | 16.0 |
| 50,000 | 0.8 | 40.0 |
| 100,000 | 0.8 | 80.0 |
| 1,000,000 | 0.8 | 800.0 |
Note: The same conversion applies; however, the three-phase system’s complexity may require additional considerations for load balancing and phase sequencing.
Detailed Explanation of Variables
Apparent Power (S in VA): Represents the total power supplied by the source, encompassing both real and reactive power. It’s calculated as:
S(VA) = V × I
Where:
V = Voltage (Volts)
I = Current (Amperes)
Power Factor (PF): A dimensionless number between 0 and 1, indicating the efficiency of the power usage. It’s the cosine of the phase angle (θ) between voltage and current waveforms:
PF = cos(θ)
PF = 1.0: Purely resistive load (e.g., incandescent lamps).
PF < 1.0: Inductive or capacitive loads (e.g., motors, transformers).
Real-World Application Examples
Example 1: Sizing a Generator for a Commercial Building
Scenario: A commercial building requires a generator to supply power to its HVAC system, lighting, and office equipment. The total apparent power demand is 150,000 VA, and the power factor is 0.85.
Calculation:
P(kW) = 150,000 VA × 0.85 / 1,000 = 127.5 kW
Conclusion: A generator with a capacity of at least 127.5 kW is necessary to meet the building’s power requirements, ensuring efficient operation without overloading.
Example 2: Determining UPS Capacity for IT Equipment
Scenario: An IT facility needs an Uninterruptible Power Supply (UPS) to support its servers. The total apparent power of the servers is 50,000 VA, and the power factor is 0.9.
Calculation:
P(kW) = 50,000 VA × 0.9 / 1,000 = 45 kW
Conclusion: The UPS should have a real power capacity of at least 45 kW to ensure continuous operation during power outages.
Reverse Conversion: kW to VA
To convert kilowatts back to volt-amperes, the formula is:
S(VA) = P(kW) × 1,000 / PF
This reverse calculation is crucial for selecting appropriately rated equipment and ensuring system compatibility.
Practical Considerations in Electrical Design
- Power Factor Correction: In systems with low power factors, installing capacitors or synchronous condensers can improve efficiency and reduce losses.
- Load Balancing: Distribute loads evenly across phases in three-phase systems to prevent overloading and ensure stable operation.
- Safety Margins: Always select equipment with a power rating higher than the calculated requirement to accommodate unforeseen surges and ensure reliability.
- Regulatory Compliance: Adhere to local electrical codes and standards (e.g., NEC, IEC) when designing and implementing electrical systems.
Advanced Formulas and Considerations for VA to kW Conversion
In complex systems, especially industrial and commercial installations, the VA to kW conversion is not always straightforward due to varying load types and system configurations. Here are the detailed formulas:
1. Single-Phase AC System
For single-phase circuits:
Where:
- V = Voltage in volts (V)
- I = Current in amperes (A)
- PF = Power factor (dimensionless)
- P = Real power in kilowatts (kW)
Notes:
- Voltage can be line-to-neutral (V_LN) in some systems. Ensure you use the correct voltage reference.
- Power factor values are typically between 0.7 (inductive motors) to 1.0 (pure resistive loads).
2. Three-Phase AC System
For three-phase systems:
Where:
- V_L = Line-to-line voltage (Volts)
- I_L = Line current (Amperes)
- PF = Power factor
- P = Real power in kilowatts (kW)
- √3 ≈ 1.732
Tip: Always verify if the system is delta or wye (star) connected; line-to-line and line-to-neutral voltage definitions differ slightly in calculations.
3. Including Efficiency (η) in Conversion
For equipment like transformers, generators, or UPS systems, efficiency must be considered:
- η = Efficiency of equipment (0 < η ≤ 1)
Example:
- A 100 kVA generator with PF = 0.85 and efficiency 0.95:
This ensures real-world accuracy in power sizing.
Extended VA to kW Conversion Table
Below is a larger reference table for common industrial and commercial loads, assuming PF = 0.8:
| VA (Volt-Amperes) | kW (Real Power) |
|---|---|
| 500 | 0.4 |
| 1,000 | 0.8 |
| 2,500 | 2.0 |
| 5,000 | 4.0 |
| 10,000 | 8.0 |
| 20,000 | 16.0 |
| 30,000 | 24.0 |
| 50,000 | 40.0 |
| 75,000 | 60.0 |
| 100,000 | 80.0 |
| 250,000 | 200.0 |
| 500,000 | 400.0 |
| 1,000,000 | 800.0 |
Tip: Use this table for quick estimates when designing systems or specifying equipment.
Additional Real-World Applications
Example 3: Industrial Motor Power Calculation
Scenario: An industrial plant uses three-phase induction motors with total apparent power demand of 200 kVA and PF = 0.75. Determine real power.
Calculation:
Conclusion: The motors require a total supply of 150 kW. Engineers should select transformers and supply lines accordingly.
Example 4: Data Center UPS Planning
Scenario: A data center has 300 kVA UPS units. Servers have a power factor of 0.92. Determine real power available.
Calculation:
Engineering Note: Always consider an additional safety margin (~10–20%) for unforeseen loads or surge capacity.
Tips for Engineering Practice
- Always consider reactive power (kVAR): Real-world systems often have inductive or capacitive loads. For total load planning, use:
Where Q = reactive power (kVAR).
- Power Factor Correction: Improving PF reduces losses and increases available real power. Industrial facilities often install capacitor banks.
- Phase Balancing: In three-phase systems, ensure loads are evenly distributed across phases to minimize neutral current and voltage drops.
- System Monitoring: Modern electrical systems use meters that provide VA, kW, and PF measurements. Always cross-check calculations with real measurements for accuracy.