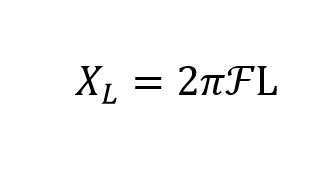With this calculator you can calculate the inductive reactance of a coil.
In addition we show the formula that is used in the conversion, definitions , tables and some explanatory examples .
Formula to calculate the inductive reactance:
The inductive reactance of an inductor depends on its inductance and the frequency that is applied. The reactance increases linearly with frequency. It is possible to express this as a formula to calculate the reactance at a particular frequency.
Where:
- ƒ = It is the frequency
- L = It is the inductance of the coil
- 2πƒ = ω
- X L = Inductive reactance
From the above equation for the inductive reactance, it can be seen that if the Frequency or the Inductance were increased, the general value of the inductive reactance would also increase. As the frequency approaches infinity, the reactance of the inductors would also increase to infinity acting as an open circuit.
However, as the frequency approaches zero or DC, the reactance of the inductors will decrease to zero, acting as a short circuit. This means that the inductive reactance is “proportional” to the frequency.
In other words, the inductive reactance increases with frequency, which means that X L is small at low frequencies and X L is high at high frequencies.
Then we can see that in DC an inductor has reactance zero (short circuit), and at high frequencies an inductor has infinite reactance (open circuit).
Inductive reactance definition:
An inductor resists the flow of an alternating current as a result of its inductance. Any inductor resists a change in the current as a result of Lenz’s Law.
The degree to which the inductor prevents current flow is due to its inductive reactance.
The inductive reactance depends on the frequency; increases with frequency, but can be easily calculated with simple formulas.
The effect by which the current flow of an alternating or changing current in an inductor is reduced is called an inductive reactance. Any current of change in an inductor will be impeded as a result of the inductance associated with it.
The reason for this inductive reactance can be seen simply by examining the autoinduction and its effect within the circuit.
When a variable current is applied to an inductor, self-induction results in an induced voltage. This voltage is proportional to the inductance and, as a result of Lenz’s law, the induced voltage is in the opposite direction to the applied voltage. In this way, the induced voltage will work against the voltage that causes the current to flow and thus prevent the flow of current.
Standard units of inductance:
| Prefix Name | Abbreviation | Weight | Henry Equivalents |
| Picohenry | pH | 10 -12 | 0.000000000001 H |
| Nanohenry | nH | 10 -9 | 0.000000001 H |
| Microhenry | μH | 10 -6 | 0.000001 F |
| Milihenry | mH | 10 -3 | 0.001 H |
| Kilohenry | kH | 10 3 | 1000 H |
These inductor values are the most common:
| Standard inductor values | |||
| nH, μH | nH, μH | nH, μH | nH, μH |
| 1.0 | 10 | 100 | 1000 |
| 1.1 | eleven | 110 | 1100 |
| 1.2 | 12 | 120 | 1200 |
| 1.3 | 13 | 130 | 1300 |
| 1.5 | fifteen | 150 | 1500 |
| 1.6 | 16 | 160 | 1600 |
| 1.8 | 18 | 180 | 1800 |
| 2.0 | twenty | 200 | 2000 |
| 2.2 | 22 | 220 | 2200 |
| 2.4 | 24 | 240 | 2400 |
| 2.7 | 27 | 270 | 2700 |
| 3.0 | 30 | 300 | 3000 |
| 3.3 | 33 | 330 | 3300 |
| 3.6 | 36 | 360 | 3600 |
| 3.9 | 39 | 390 | 3900 |
| 4.3 | 43 | 430 | 4300 |
| 4.7 | 47 | 470 | 4700 |
| 5.1 | 51 | 510 | 5100 |
| 5.6 | 56 | 560 | 5600 |
| 6.2 | 62 | 620 | 6200 |
| 6.8 | 68 | 680 | 6800 |
| 7.5 | 75 | 750 | 7500 |
| 8.2 | 82 | 820 | 8200 |
| 8.7 | 87 | 870 | 8700 |
| 9.1 | 91 | 910 | 9100 |
How to calculate the inductive reactance in 1 single step:
Step 1:
To calculate the inductive reactance of an inductor, multiply 2 by the number pi (π), by frequency and inductance
Example: An inductor of 55mH, has a frequency of 50Hz, which is its inductive reactance, to find the answer it must be multiplied: 2xπx50x55x10 ^ -3 = 17,28Ohm
Examples of inductive reactance calculations:
Example of inductive reactance No1:
A coil has an inductance of 0.5H. What will be the value of the inductive reactance, if the coil has a frequency of 100Hz?
Rta: // This is a theoretical example because in reality the coils have a resistive + inductive component, for our case we only have to multiply the variables of the formula in the following way: 2xπx100x0,5 = 314,16 Ohm.
Example of inductive reactance No2:
A solenoid coil has an inductance of 240nF and a frequency of 10000Hz. Calculate the inductive reactance of the coil.
RTA: // The inductive reactance knowing that the frequency is 800Hz is calculated as follows: 2xπx240x10 ^ -9 × 10000 = 0.02 Ohm.
Example of inductive reactance No3:
an 8H inductor is connected to a circuit at a frequency of 60Hz. Calculate the inductive reactance of this circuit ?.
Rta: // The calculation, like the previous ones, uses the formula and the calculator, the result should be: 3015.93 Ohm.