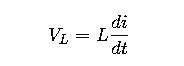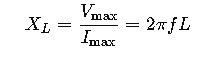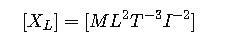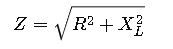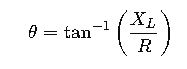Inductive reactance (XL) is a key property in AC circuits, opposing current flow through inductors. This effect occurs because inductors store energy magnetically, releasing it, critical for efficient system design.
Inductive Reactance Calculator (XL)
What formula is used?
What is inductive reactance?
Inductive Reactance Formula
The inductive reactance is calculated using the formula:

Derivation and Explanation
The formula XL=2πfL is derived from the relationship between voltage and current in an inductor. According to Faraday’s Law of Induction, the voltage (VL) across an inductor is proportional to the rate of change of current (di/dt):
For a sinusoidal current i(t)=Imaxsin(2πft), the rate of change is di/dt=2πfImaxcos(2πft). The peak voltage is then Vmax=2πfLImax. The inductive reactance represents the ratio of the peak voltage to the peak current:
Units and Dimensions
The inductive reactance XL has the same units as resistance, which is ohms (Ω). Its dimensional formula is:
This indicates that inductive reactance depends on the inductance of the coil and the frequency of the AC signal.
Common Values of Inductive Reactance
Below is a table illustrating the inductive reactance for various inductance values and frequencies:
| Frequency (Hz) | Inductance (H) | Inductive Reactance (Ω) |
|---|---|---|
| 50 | 0.001 | 0.314 |
| 50 | 0.01 | 3.14 |
| 50 | 0.1 | 31.4 |
| 50 | 1 | 314 |
| 100 | 0.001 | 0.628 |
| 100 | 0.01 | 6.28 |
| 100 | 0.1 | 62.8 |
| 100 | 1 | 628 |
| 1000 | 0.001 | 6.28 |
| 1000 | 0.01 | 62.8 |
| 1000 | 0.1 | 628 |
| 1000 | 1 | 6280 |
This table demonstrates how inductive reactance increases with both frequency and inductance. For instance, at 50 Hz, an inductor with 0.1 H inductance has a reactance of 31.4 Ω, while at 1000 Hz, the same inductor’s reactance increases to 628 Ω.
Real-World Applications of Inductive Reactance
1. Power Factor Correction in Industrial Systems
In industrial settings, large motors and transformers often introduce inductive reactance into the power system, leading to a phase difference between voltage and current. This phase difference reduces the efficiency of power delivery. By calculating the inductive reactance and installing capacitors with appropriate reactance values, the overall reactance can be minimized, improving the power factor and enhancing system efficiency.
2. Design of Radio Frequency (RF) Circuits
In RF circuits, inductive reactance is used to filter signals at specific frequencies. By selecting inductors with the appropriate inductance values, engineers can design circuits that resonate at desired frequencies, allowing for selective signal processing. For example, in a band-pass filter, the inductive reactance at the resonant frequency is matched with the capacitive reactance to allow signals within a certain frequency range to pass while attenuating others.
Advanced Considerations
Impedance in R-L Circuits
In circuits containing both resistive and inductive elements, the total opposition to current flow is termed impedance (Z). The impedance in an R-L series circuit is given by:
Where R is the resistance and XL is the inductive reactance. The phase angle (θ) between the voltage and current is:
These equations are crucial for analyzing the behavior of AC circuits and designing systems with desired impedance characteristics.
Skin Effect at High Frequencies
At high frequencies, the skin effect causes the current to concentrate near the surface of conductors, effectively reducing the cross-sectional area available for current flow. This phenomenon increases the effective resistance and reactance of conductors. Engineers must account for the skin effect when designing high-frequency circuits to ensure accurate impedance matching and efficient signal transmission.
Key Takeaways
Inductive reactance is a fundamental parameter in AC circuit analysis and design. By understanding its calculation and implications, engineers can design more efficient electrical systems, from power distribution networks to advanced electronic devices. Accurate calculation and consideration of inductive reactance are essential for optimizing performance and ensuring the reliability of electrical systems.