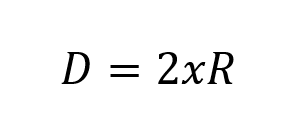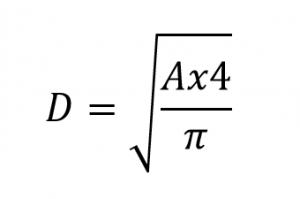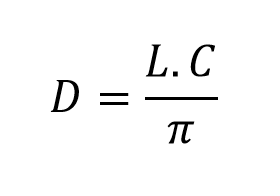There are three ways to calculate the diameter of a circumference, by means of the area, the radius or the length of the circumference.
The simplest way to calculate the diameter of a circle is by means of the following diameter calculator.
Formulas for the calculation of the diameter of a circumference:
1. Formula for the calculation of the diameter from the radius. The following equation describes the relationship between the diameter and the radius R of a circumference:
Where:
- r: Radius of the circumference.
- D: Diameter.
2. Formula for the calculation of the diameter from the Area. An equally simple formula determines the relationship between the diameter and the area of a circle:
Where:
- A: Area of the circle.
- D: Diameter.
- π: Constant Number equivalent to 3.1415
3. Formula for the calculation of the diameter from the length of the circumference. This formula with the same simplicity of the others relates the diameter with the length of the circumference:
Where:
- LC: Length of the circumference.
- D: Diameter.
- π: Constant Number equivalent to 3.1415
How to find the diameter of a circumference:
As you can see there are three ways to calculate the diameter of a circumference, the method you use of the following three will depend on the data you have (Radius, area or circumference length):
– How to calculate the diameter of a circle when you have the radius:
Step a. The radio data is indispensable in this method, the value is a numerical constant. Let’s suppose that the radius is equal to 45 meters.
Step b. Substitute the previous value in formula No. 1, which depends on the radius: D = 2xR = 2 × 45 = 90 meters.
– How to calculate the diameter of a circle when you have the area:
Step a. In this method of calculation you must have the area of the circle. In our case we are going to assume an area of 200cm ^ 2.
Step b. You must replace in the formula that depends on the bone area the No2. as follows: D = √ ((Ax4) / π) = (200 × 4) / 3.1415 = 15.96cm. If you are a retailer you will notice that the area is given with the distance squared (cm ^ 2), while the length (Diameter) is given in “cm”.
– How to calculate the diameter of a circle when you have the length of the circumference:
Step a. The length of the circumference is indispensable for this way of calculating the diameter. We are going to assume a valos of length of circumference of 32mm.
Step b. Like all the previous methods, this is the same, it is simple. You only have to replace the formula No 3, in the following way: LC / π = 32 / 3.1415 = 10.19mm.
Most important definitions:
Diameter: The diameter of a circle or circumference is the length of the line that passes through the center and touches two points on its edge.
The diameter is also a chord. A chord is a line that joins two points in a circle. A diameter is a string that extends through the center point of the circle. It is the longest possible chord of any circle.
The center of a circle is the midpoint of its diameter. That is, it divides it into two equal parts, each of which is a radius of the circle. The radius is half the diameter.
Circumference: The circumference is the distance around the edge of the circle.
Circle: A circle is a shape with all points at the same distance from the center. If you measure the distance around a circle and divide it by the distance through the circle passing through the center, you will always approach a particular value, depending on the accuracy of your measurement. This value is approximately 3.14159265358979323846 … the Greek letter pi (pronounced Pi) is used to represent this value.
Radio: A basic definition is the distance from the center to the edge.
Number “pi” π: Pi is the name given to the relation of the circumference of a circle and the diameter. That means that, for any circle, you can divide the circumference (the distance around the circle) by the diameter and always get the same number. No matter how big or small the circle is, Pi remains the same.
Length of the circumference: See definition circumference.
Area of the circumference: Informally we could say that the area of a circle, are all the points that are enclosed in the circle. It is all that has a circle inside it.
[kkstarratings]