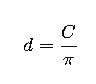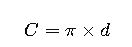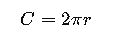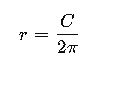Understanding the relationship between a circle’s circumference and diameter is essential in geometry, engineering, and science. This guide explores formulas, practical applications, and detailed real-world examples of circumference-diameter calculations.
Circumference ↔ Diameter Calculator
Formulas used
Circumference → Diameter: D = C / π
Table of Common Circumference and Diameter Values
| Diameter (inches) | Circumference (inches) | Diameter (mm) | Circumference (mm) |
|---|---|---|---|
| 1 | 3.1416 | 25.4 | 79.787 |
| 2 | 6.2832 | 50.8 | 157.574 |
| 3 | 9.4248 | 76.2 | 235.361 |
| 4 | 12.5664 | 101.6 | 313.148 |
| 5 | 15.7080 | 127.0 | 391.935 |
| 6 | 18.8496 | 152.4 | 470.722 |
| 7 | 21.9912 | 177.8 | 549.509 |
| 8 | 25.1328 | 203.2 | 628.296 |
| 9 | 28.2744 | 228.6 | 707.083 |
| 10 | 31.4160 | 254.0 | 785.870 |
| 12 | 37.6992 | 304.8 | 956.448 |
| 15 | 47.1240 | 381.0 | 1196.918 |
| 20 | 62.8320 | 508.0 | 1595.928 |
| 25 | 78.5400 | 635.0 | 1994.680 |
| 30 | 94.2480 | 762.0 | 2393.568 |
| 50 | 157.0800 | 1270.0 | 3981.960 |
| 100 | 314.1600 | 2540.0 | 7963.920 |
Note: Circumference values are calculated using π ≈ 3.1416. Values are rounded to four decimal places for precision.
Fundamental Formulas for Circumference-Diameter Calculations
1. Circumference to Diameter
- Formula:
- Explanation:
- d= Diameter of the circle
- C = Circumference of the circle
- π≈3.1416 (Mathematical constant representing the ratio of circumference to diameter)
This formula allows the calculation of a circle’s diameter when its circumference is known. It is extensively applied in manufacturing, construction, and material cutting processes where exact diameter measurement is critical.
2. Diameter to Circumference
- Formula:
- Explanation:
- C= Circumference of the circle
- d= Diameter of the circle
This formula determines the perimeter of a circle based on its diameter. It is essential in design, engineering, and quality control to measure circular objects and components accurately.
3. Circumference from Radius
- Formula:
- Explanation:
- C= Circumference of the circle
- r= Radius of the circle (d=2r)
This formula is widely used in physics, engineering, and computer graphics, particularly when the radius is the known dimension of a circle. It is vital for calculating perimeters of circular paths, disks, and wheels.
4. Diameter from Radius
- Formula:
d=2r
- Explanation:
- d= Diameter of the circle
- r= Radius of the circle
A straightforward relationship that is essential in trigonometry, geometry, and any calculation requiring the transition between radius and diameter.
5. Radius from Circumference
- Formula:
- Explanation:
- r= Radius of the circle
- C= Circumference of the circle
This formula is crucial in reverse engineering and measurement tasks where only the perimeter is known, and the radius needs to be derived.
Extended Table of Diameter-Radius-Circumference Relationships
| Diameter (inches) | Radius (inches) | Circumference (inches) | Diameter (mm) | Radius (mm) | Circumference (mm) |
|---|---|---|---|---|---|
| 1 | 0.5 | 3.1416 | 25.4 | 12.7 | 79.787 |
| 2 | 1 | 6.2832 | 50.8 | 25.4 | 157.574 |
| 3 | 1.5 | 9.4248 | 76.2 | 38.1 | 235.361 |
| 4 | 2 | 12.5664 | 101.6 | 50.8 | 313.148 |
| 5 | 2.5 | 15.7080 | 127.0 | 63.5 | 391.935 |
| 6 | 3 | 18.8496 | 152.4 | 76.2 | 470.722 |
| 8 | 4 | 25.1328 | 203.2 | 101.6 | 628.296 |
| 10 | 5 | 31.4160 | 254.0 | 127.0 | 785.870 |
| 12 | 6 | 37.6992 | 304.8 | 152.4 | 956.448 |
| 15 | 7.5 | 47.1240 | 381.0 | 190.5 | 1196.918 |
| 20 | 10 | 62.8320 | 508.0 | 254.0 | 1595.928 |
| 25 | 12.5 | 78.5400 | 635.0 | 317.5 | 1994.680 |
| 30 | 15 | 94.2480 | 762.0 | 381.0 | 2393.568 |
| 50 | 25 | 157.0800 | 1270.0 | 635.0 | 3981.960 |
| 100 | 50 | 314.1600 | 2540.0 | 1270.0 | 7963.920 |
Real-World Applications
1. Manufacturing of Circular Components
In industrial manufacturing, such as automotive, aerospace, and machinery, precise circumference-diameter calculations are vital. When creating circular components like gears, wheels, and bearings, accuracy in diameter ensures proper fit and function.
- Example Case:
A wheel rim has a diameter of 18 inches. Using the formula C=π×d:
This circumference is required to cut a strip of metal for forming the wheel rim. The accuracy of the calculation directly affects the rim’s roundness and fit with tires.
2. Civil Engineering: Pipes and Tunnels
Engineers must calculate pipe diameters and tunnel perimeters for fluid flow, material cost estimation, and structural integrity. The relationship between circumference and diameter helps determine volumes, pressures, and capacities.
- Example Case:
A drainage pipe has a measured circumference of 62.832 inches. To determine the diameter:
This calculation enables accurate assessment of water flow capacity and ensures compatibility with other plumbing components.
3. Robotics and Motion Systems
Circular motion components, such as wheels, pulleys, and rotating disks in robotics, require precise circumference-diameter calculations to program accurate movement paths. Using these formulas ensures correct motion distance per rotation.
- Example Case:
A robot wheel radius = 5 inches. Circumference:
This circumference defines the distance the robot moves per full wheel rotation, crucial for navigation and path planning.
Additional Considerations
- Precision of π: For high-precision engineering or scientific applications, π should be used to more decimal places (3.1415926535…) to avoid cumulative errors in large structures.
- Unit Consistency: Ensure all values are in the same measurement units (inches, millimeters, or centimeters) to prevent miscalculations.
- Complex Geometries: For elliptical or non-circular components, alternative formulas involving ellipse circumference approximations or CAD tools may be necessary.
- Material Planning: Circumference calculations are critical for determining material lengths, cutting patterns, and cost estimation in manufacturing.
- Quality Control: Ensuring the calculated diameter matches measured circumference verifies product tolerances and roundness.
This comprehensive guide provides the formulas, tables, and practical insights required for precise circumference-diameter calculations across various industries, from manufacturing and civil engineering to robotics and design. Accurate application of these principles ensures efficiency, cost-effectiveness, and structural reliability.