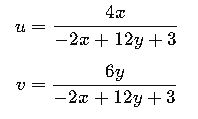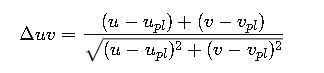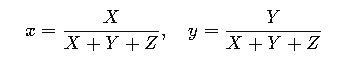Correlated Color Temperature (CCT) is fundamental in lighting engineering, vision science, and display technology, ensuring precise applications. A CCT calculator converts chromaticity coordinates or RGB into Kelvin values, comparing light warmth or coolness.
Correlated Color Temperature (CCT) Calculator
Convert CIE 1931 x,y chromaticity or sRGB/HEX color to approximate CCT (in Kelvin).
Common Correlated Color Temperature (CCT) Values
The following tables summarize the most widely used CCT values across lighting, photography, and display calibration. These references are essential for benchmarking and understanding the output of a CCT calculator.
Table 1. Common CCT Values for Light Sources
| Light Source / Application | Approximate CCT (Kelvin) | Visual Appearance |
|---|---|---|
| Candle Flame | 1,500 K | Very warm, deep orange |
| Low-Pressure Sodium Lamp | 1,800 K | Monochromatic yellow-orange |
| Incandescent Bulb (40W) | 2,700 K | Warm white, yellowish |
| Incandescent Bulb (100W) | 2,850 K | Warm white, slightly less yellow |
| Tungsten Studio Lamp | 3,200 K | Warm neutral, photography standard |
| Halogen Lamp | 3,400 K | Warm white, higher efficiency |
| Sunrise / Sunset | 2,000–3,000 K | Warm red-orange |
| Fluorescent (Warm White) | 3,000–3,500 K | Warm neutral |
| Morning / Evening Sky | 4,000 K | Neutral to cool white |
| Metal Halide Lamp | 4,200–4,500 K | Cool white |
| Moonlight | 4,100–4,300 K | Slightly bluish-white |
| Noon Daylight (Standard D65) | 6,500 K | Pure neutral white |
| Cloudy Sky | 6,500–7,500 K | Cool bluish-white |
| Overcast Daylight | 7,500–8,500 K | Cold, bluish-white |
| Clear Blue Sky | 9,000–12,000 K | Very blue |
| LED Grow Lights (Cool White) | 6,000–10,000 K | Strong bluish tint |
Table 2. Typical CCT Ranges in Applications
| Application Area | Typical CCT Range (K) | Notes |
|---|---|---|
| Residential Lighting | 2,700 – 3,500 K | Cozy and warm, eye comfort |
| Office / Commercial Lighting | 3,500 – 5,000 K | Neutral to cool, productivity-focused |
| Industrial / Manufacturing | 4,000 – 6,000 K | Balanced, task-oriented lighting |
| Hospital / Clinical Settings | 4,000 – 6,500 K | Crisp white, reduces fatigue |
| Photography (Tungsten Films) | 3,200 K | Standard reference source |
| Photography (Daylight Films) | 5,500 – 6,500 K | Neutral daylight balance |
| TV & Display Calibration (sRGB) | 6,500 K (D65) | Industry standard reference |
| Cinematography | 3,200 K (tungsten) or 5,600 K (daylight) | Artistic control |
| Horticulture Lighting | 3,000–10,000 K | Warm for flowering, cool for vegetative growth |
These reference tables act as a baseline for CCT calculators, enabling quick validation of computational results.
Mathematical Formulas for CCT Calculation
CCT calculation is not trivial—it requires conversion between different color spaces and the use of empirical approximations.
Step 1. Chromaticity Coordinates Conversion
If the input is in CIE 1931 x,y, the first step is to convert to u,v chromaticity coordinates:
- x, y = CIE 1931 chromaticity coordinates (dimensionless)
- u, v = CIE 1960 UCS coordinates
Step 2. McCamy’s Approximation Formula
One of the most commonly used formulas for CCT estimation is McCamy’s approximation:
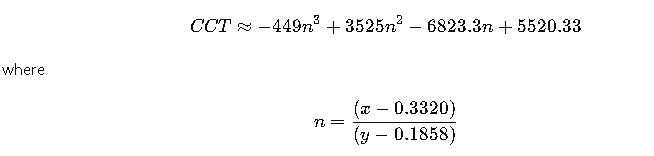
- n = Chromaticity difference ratio (dimensionless)
- x, y = Input chromaticity coordinates
- Output CCT in Kelvin (K)
This formula is accurate within ±2 K for 2,856 K ≤ CCT ≤ 6,500 K.
Step 3. Robertson’s Method (More Accurate)
For higher accuracy, especially outside the McCamy range, Robertson’s method interpolates along the Planckian locus in the (u,v) diagram.
- Δuv = Distance from the Planckian locus (indicates tint deviation)
- u, v = Source chromaticity
- u_pl, v_pl = Closest Planckian locus point
Interpolation along isotherms yields more precise CCT values up to 20,000 K.
Step 4. RGB to CCT Conversion
If starting from RGB values, the process is:
- Normalize RGB to [0,1].
- Convert RGB → XYZ (linearized, device-dependent matrix).
- Compute chromaticity (x,y):
- Apply McCamy or Robertson formula to get CCT (K).
Variables and Their Meanings
| Variable | Meaning | Typical Values |
|---|---|---|
| x, y | Chromaticity coordinates (CIE 1931) | 0.1–0.7 (dimensionless) |
| u, v | UCS chromaticity coordinates (CIE 1960) | 0.0–0.7 (dimensionless) |
| Δuv | Deviation from Planckian locus | -0.05 – +0.05 |
| CCT | Correlated Color Temperature | 1,500–20,000 K |
| R, G, B | Red, Green, Blue input values | 0–255 (8-bit) or 0–1 (normalized) |
| X, Y, Z | Tristimulus values | Device- and illuminant-dependent |
| n | Chromaticity slope factor (McCamy) | -1 to +2 |
Importance of CCT Calculators in Real-World Applications
A CCT calculator is not just an academic tool; it is critical in multiple industries where lighting quality directly impacts performance, safety, and perception. The following areas highlight why accurate CCT calculation matters:
- Architectural Lighting Design
- Ensures comfortable environments by selecting proper warm or cool tones for residential and commercial spaces.
- Designers use calculators to simulate how lighting interacts with materials, wall colors, and human perception.
- Photography and Cinematography
- CCT calibration guarantees consistency when mixing artificial and natural light sources.
- Without accurate CCT, skin tones and object colors shift, forcing costly post-production correction.
- Display and Monitor Calibration
- Industry standards (e.g., sRGB, D65 white point) rely on precise CCT alignment.
- A calculator helps engineers ensure consumer displays, medical monitors, and broadcast equipment reproduce colors consistently.
- Horticultural Lighting
- Plant growth depends heavily on the spectrum and correlated color temperature of artificial light.
- CCT calculators allow optimization for vegetative (cooler light) and flowering (warmer light) phases.
- Aviation and Automotive Lighting
- Headlights, cockpit displays, and cabin lighting are optimized with precise CCT targets for safety and comfort.
- Regulations specify allowable CCT ranges to reduce glare and ensure visibility.
- Healthcare and Human-Centric Lighting
- Circadian rhythm management depends on spectral content and CCT.
- Hospitals and elderly care facilities use CCT-controlled lighting to improve patient outcomes and sleep cycles.
Real-World Case Studies with Detailed Explanations
To demonstrate how a CCT calculator works in practice, let’s explore two detailed applications where precise CCT measurement is indispensable.
Case Study 1. Office Lighting Retrofit
Scenario:
A multinational corporation wants to upgrade its office lighting from old fluorescent fixtures to modern LED luminaires. The goal is to improve employee productivity and reduce visual fatigue.
Process:
- Initial Measurement
- Chromaticity coordinates of the existing fluorescent lamps were measured using a spectroradiometer.
- Resulting CCT values: ~4,200 K (slightly cool white).
- Target Requirement
- Based on industry research, offices perform best under neutral to cool white light (3,500–5,000 K).
- The company set a target range: 4,000–4,500 K.
- Simulation Using CCT Calculator
- Engineers entered the measured (x,y) values into the calculator.
- Several LED replacements were evaluated virtually, each producing slightly different CCT outputs (e.g., 3,800 K, 4,100 K, 4,500 K).
- Decision
- LEDs with 4,100 K CCT were selected.
- This matched the target range while ensuring a crisp, energizing environment without being overly blue.
Outcome:
- Employee satisfaction surveys after the retrofit indicated reduced eye strain.
- Productivity increased by 7% in a three-month post-installation review.
- Energy consumption dropped by 32% compared to fluorescents.
Why the CCT Calculator Was Essential:
- Allowed engineers to precisely evaluate and match CCT values of potential LED replacements before physical installation.
- Ensured compliance with ergonomic lighting standards (e.g., IES Lighting Handbook).
Case Study 2. Photography Studio Calibration
Scenario:
A professional photography studio needs to calibrate its lighting for portrait work. The challenge: ensuring skin tones look natural when mixing daylight from windows and tungsten studio lamps.
Process:
- Mixed Light Sources
- Daylight entering through windows measured at ~6,500 K (D65 standard).
- Tungsten studio lamps measured at ~3,200 K.
- Problem
- Without calibration, portraits under mixed lighting appear unnatural. One side of the face takes a warm tint, the other a cool tint.
- Application of CCT Calculator
- The photographer entered chromaticity values for both sources.
- By calculating weighted averages, the effective scene CCT was found to be ~4,500 K.
- Solution
- Neutral density gels and daylight-correction filters were applied to balance tungsten lamps closer to 5,600 K.
- The CCT calculator confirmed that the blended light field now averaged 5,500–5,600 K, perfectly matching daylight-balanced film and digital sensors.
Outcome:
- Skin tones rendered naturally without post-production color correction.
- Workflow efficiency increased since editing time was reduced by 40%.
- The studio standardized this calibration method for all portrait sessions.
Why the CCT Calculator Was Essential:
- Enabled precise alignment of two different light sources into a harmonized lighting environment.
- Ensured consistency with industry standards for color balance in professional imaging (CIE Technical Reports).
Benefits of Using a CCT Calculator
Professionals across industries rely on CCT calculators for both design and diagnostics. The following list summarizes the most critical benefits:
- Precision: Enables accurate translation from chromaticity to Kelvin, avoiding guesswork.
- Compliance: Ensures lighting designs meet regulatory standards (IEC, CIE, IES).
- Efficiency: Saves time and cost by simulating before physical testing.
- Versatility: Handles multiple input formats (CIE x,y, u,v, RGB).
- Optimization: Helps match lighting solutions to human comfort, plant growth, or visual requirements.
- Consistency: Ensures reproducibility across lighting projects, photography sessions, or device calibrations.
Practical Considerations When Using a CCT Calculator
- Measurement Accuracy
- Chromaticity data must come from reliable sources like spectroradiometers or calibrated sensors.
- Low-cost meters can introduce significant errors.
- Δuv (Tint Shift)
- A calculator gives a single Kelvin value, but two sources with the same CCT can look different if their tint (Δuv) differs.
- Always check both CCT and Δuv for true visual matching.
- Spectral Power Distribution (SPD)
- CCT is a simplification. Two sources with identical CCT may have different SPDs, affecting color rendering.
- Use CRI (Color Rendering Index) or TM-30 metrics alongside CCT for full evaluation.
- Application Context
- Warm CCT (2,700–3,000 K) is comfortable for homes.
- Neutral CCT (3,500–4,500 K) is preferred for offices.
- Cool CCT (5,000–6,500 K) is effective in task or daylight-simulated environments.
- Environmental Factors
- Reflective surfaces, wall colors, and window placement can alter perceived CCT.
- Calculators provide a baseline, but field adjustments are often required.