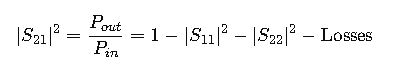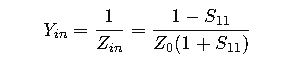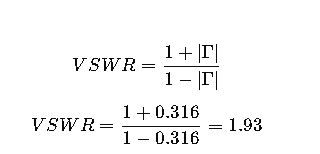In high-frequency design, converting scattering parameters into impedance enables practical circuit analysis and optimization. S11 and S21 are essential, linking input impedance, reflection coefficient, and transmission behavior in RF networks.
S-Parameters → Impedance Calculator (S11)
How is impedance calculated from S11?
Can I input complex numbers?
Normalized vs Absolute Impedance
Why Converting S-Parameters to Impedance Matters
- Practical interpretation: Impedance is easier to interpret in terms of voltage, current, and power transfer.
- Design optimization: Network matching requires impedance values, not S-parameters alone.
- Measurement translation: VNAs (Vector Network Analyzers) measure S-parameters, but engineers often require impedance for component or system-level integration.
- System interoperability: Impedance ensures compatibility between components in RF systems, antennas, and transmission lines.
S-Parameters and Their Role
S-parameters describe how RF signals behave in terms of incident and reflected waves.
- S11: Reflection coefficient at port 1, representing how much of the signal is reflected back.
- S21: Forward transmission coefficient from port 1 to port 2, representing signal transmission efficiency.
While S21 is mainly related to gain/loss, it can also indirectly provide impedance-related insights when considered alongside other parameters.
Core Formulas for Converting S-Parameters to Impedance
Input Impedance from S11
The input impedance Zin of a one-port or multi-port device can be derived from S11:

Reflection Coefficient to Impedance Conversion
Since S11 is equivalent to the reflection coefficient Γ:

Impedance from S21 (Indirect Method)
Although S21 is not directly converted into impedance, its magnitude and phase provide information about power transmission, which can be combined with S11 to characterize impedance transformation networks. For example:
In impedance-matching networks, S21 is often analyzed with S11 to ensure proper input-output impedance transformation.
Admittance Conversion
Sometimes, admittance is more convenient than impedance:
This is particularly useful in Smith Chart analysis.
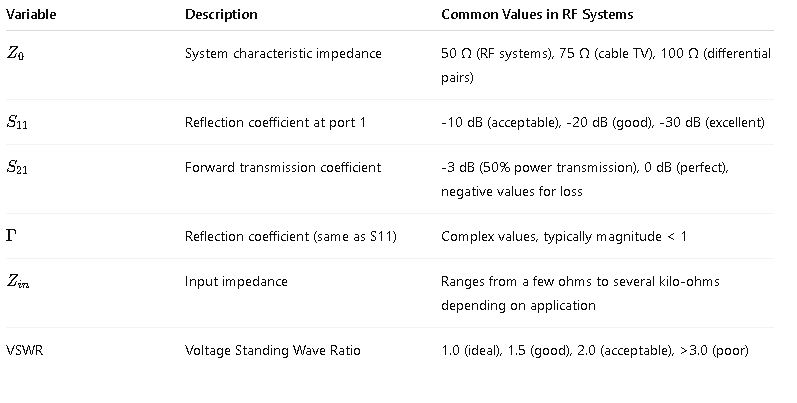
Variables and Their Common Values
Extensive Lookup Tables
The following tables present common conversion values between S11, reflection coefficient, VSWR, and input impedance for a 50 Ω system.
Table 1: S11 (Magnitude in dB) to Reflection Coefficient and VSWR
| S11 (dB) | Reflection Coefficient (|Γ|) | VSWR | Approximate Return Loss Quality |
|———-|————————–|——|——————————–|
| -3 dB | 0.707 | 5.83 | Poor |
| -6 dB | 0.501 | 3.01 | Marginal |
| -10 dB | 0.316 | 1.92 | Acceptable |
| -15 dB | 0.178 | 1.43 | Good |
| -20 dB | 0.100 | 1.22 | Very Good |
| -30 dB | 0.0316 | 1.06 | Excellent |
| -40 dB | 0.010 | 1.02 | Outstanding |
Table 2: Reflection Coefficient to Impedance (for Z0 = 50 Ω)
| Reflection Coefficient (Γ) | Real Impedance (Ω) | Imaginary Impedance (Ω) | Comment |
|---|---|---|---|
| 0.0 | 50 | 0 | Perfect match |
| 0.2 | 75 | 0 | Mild mismatch |
| 0.5 | 150 | 0 | Significant mismatch |
| -0.2 | 33.3 | 0 | Lower than 50 Ω |
| -0.5 | 16.7 | 0 | Severe mismatch |
| j0.5 | 50 | +50 | Inductive reactance |
| -j0.5 | 50 | -50 | Capacitive reactance |
Table 3: S11 to Input Impedance (Z0 = 50 Ω)
| S11 Value | Input Impedance (Ω) |
|---|---|
| 0.1 | 61.1 Ω |
| 0.2 | 75 Ω |
| 0.3 | 92.9 Ω |
| 0.5 | 150 Ω |
| -0.1 | 45.5 Ω |
| -0.2 | 41.7 Ω |
| -0.5 | 33.3 Ω |
Case Studies and Real-World Applications
Case Study 1: Impedance Matching for a 2.4 GHz Antenna
Problem
A Wi-Fi antenna operating at 2.4 GHz is measured with a Vector Network Analyzer (VNA). The measured S-parameter at the operating frequency is:
- S11=−10 dB
- S21=−1.2 dB
The system characteristic impedance is Z0=50Ω. Determine the input impedance of the antenna and assess whether it is properly matched.
Step 1: Convert S11 from dB to Linear

Step 2: Impedance Calculation
The general formula is:
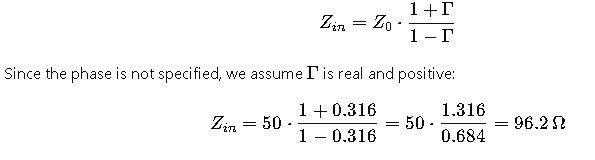
Step 3: VSWR Calculation
Step 4: Transmission Loss with S21
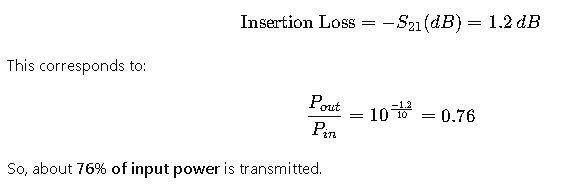
Assessment
- Input impedance is 96.2 Ω, higher than 50 Ω.
- VSWR of 1.93 indicates moderate mismatch.
- Transmission efficiency of ~76% is acceptable but not optimal.
Solution: The antenna requires a matching network (e.g., an L-network or Smith Chart-based design) to bring its impedance closer to 50 Ω for better performance.
Extended Conversion Tables
To aid engineers in practical design, below are additional lookup values for quick conversions.
Table 4: Common Return Loss to Reflection Coefficient and VSWR
| Return Loss (dB) | Reflection Coefficient (|Γ|) | VSWR | Power Reflected (%) |
|——————|————————–|——|———————-|
| 5 dB | 0.562 | 3.6 | 31.6% |
| 10 dB | 0.316 | 1.92 | 10% |
| 15 dB | 0.178 | 1.43 | 3.16% |
| 20 dB | 0.100 | 1.22 | 1% |
| 30 dB | 0.0316 | 1.06 | 0.1% |
| 40 dB | 0.010 | 1.02 | 0.01% |
Table 5: S11 to Input Impedance for Z0 = 50 Ω (Extended)
| S11 | Input Impedance (Ω) |
|---|---|
| -0.05 | 47.6 Ω |
| -0.1 | 45.5 Ω |
| -0.2 | 41.7 Ω |
| -0.3 | 38.5 Ω |
| 0.1 | 61.1 Ω |
| 0.2 | 75 Ω |
| 0.3 | 92.9 Ω |
| 0.4 | 116.7 Ω |
| 0.6 | 200 Ω |
Practical Engineering Applications
- Antenna Design: Ensuring antennas are matched to 50 Ω to maximize radiated power.
- Transmission Line Design: Verifying PCB microstrip or coaxial lines maintain impedance uniformity.
- Filter Design: Using S21 to characterize band-pass, band-stop, and low-pass filters.
- Amplifier Stability: Using S11 to confirm amplifiers are matched and stable under load variations.
- Medical Imaging (MRI coils): Precise impedance matching ensures maximum power transfer from RF amplifiers.
- 5G and IoT Systems: Proper S-parameter to impedance conversion guarantees device interoperability.
References and Authoritative Sources
- Keysight: Understanding S-parameters
- IEEE Xplore: Advanced impedance matching techniques
- National Instruments: RF Measurements and S-parameters
- [Pozar, D. M., Microwave Engineering, 4th Edition]