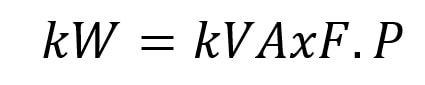⚡Calculator☝Formula🎯table🏭power factor✍Examples🤷♂️How to convert💡KW to KVA
⚡Formula from kVA to kW.
Commonly of the two variables required by the formula ( kVA and FP ), the variable that is more difficult to achieve is the power factor, however on our page we provide this information through the fp table .
Where:
- kW: Power is called real and designated with the letter “P”, is the value to be found. .
- kVA: Call apparent power and designated with the letter “S”.
- Power factor: Defines the efficiency of an electrical system.
☝How to convert, pass or transform from kVA to kW in 1 step.
To convert from kVA to kW you must have two variables : kVA and power factor, then you must simply multiply kVAx Power factor , as reported by the formula and the result of this multiplication will be the kW.
The kVA and the Power Factor are commonly found on the nameplate of the inductive electrical equipment (see figure 1), mainly generators, keep in mind that the power factor can also appear as cos (φ) . In this case, figure 1 shows the characteristic plate of a 570kVA generator and a power factor of 0.8.
In reality, most of the characteristic plates of the electrical equipment do not have the kVA because the common designation is made in kW , this is partly because many of them despise the power factor because they are very efficient electrical equipment , without However, this does not mean that the equipment does not have fp, on the contrary most of the equipment that works with AC voltage has a power factor, so if the plates do not inform you of the fp we show you the tables with the most common values the power factors for different engines, constructions and equipment in general.
Step 1.
This calculation is done simply by multiplying the kVA by the load power factor , if you do not know the latter you can use the ones shown here .
Example , To avoid running out of energy, a mine uses an electric generator, which has a prime power of 74.6kVA , this equipment has a power factor of 0.87 , knowing the above, how much power in kW can this equipment deliver ? , to know the answer you just have to multiply 74.6kVA by 0.87 which will result in: 64.9kW. (74.6kVAx0.87 = 64.9kW).
In reality the power factor delivered by a generator depends on the load and is limited by the capacity of the generator, this means that if the generator is built to deliver 800kVA / 640kW at a power factor of 0.8, it cannot deliver 750kVA / 562kW at a power factor of 0.75. Therefore it is important to respect the limits of both kVA , kW and power factor of the generators and the load.
It is important to know that kW will always be less than kVA, this is because the power factor is always less than 1 (from 0 to 1), so the multiplication of kVAxF.P = kW will never result in a value greater than kVA (kW≤kVA).
✍Examples and exercises.
Example 1 – Convert the kVA of an extractor to kW:
An air extractor in a warehouse has a power of 5kVA , with a power factor of 0.85 and is connected to a panel with a voltage of 220V, how many kW does the extractor have ?
Rta: // To get the answer you just have to take the kVA and multiply them by the power factor , as follows: 5kVAx0.85, obtaining 4.25kW, in other words kW = 5kVAx0.85 = 4.25kW , for the conversion The formula from kVA to kW was used above.
As you can see the kVA are always greater than the kW , this is because the power factor is always less than 1, it is common that the equipment is not marked with the kVA but with the kW and does not have the power factor However, there are tables with typical power factors for many electrical equipment .
Example 2 – How to bring kVA to kW for a bakery oven:
It has a resistive load of an 80kVA oven with a power factor of 1 and a voltage of 4160Volts , how many kW is the oven ?
Rta: // To know the answer you must multiply kVAx Power factor , as in the previous example, with which you will have 80kVAx1, which is equal to 80kW, as you can commonly see resistive loads have kVA equal to kW (kVA = kW, in resistive loads).
Example 3 – Transform the AA load from kVA to kW:
An inductive load of an air conditioner has a power of 25kVA , with a power factor of 0.83 , what will be the power in kW of the air conditioner ?
Rta: // You should only multiply 25kVAx0.83 , which will result in 20.75kW, as you can see in inductive loads such as motors, transformers, computers, elevators, air conditioners and in general equipment with motors and electronics has power factors below 1 , which would ensure that the kVA of this equipment is greater than kW.
It is common for energy service companies to penalize the power factor that is below 1.
🎯Tables from kVA to kW transformers, generators, UPS and other equipment.
These tables report the equivalences of kVA to kW for standard sizes of single-phase, two-phase and three-phase equipment, both transformers, generators, UPS and other electrical equipment, the calculation basis for the conversion is a power factor of 0.8, for different values the calculator from kVA to kW must be used.
Table of kVA to kW for three-phase transformers (Power factor of 0.8):
The transformers are designated by kVA and not by kW, this is because the transformers can have almost any kW and the latter will depend on the load, for example, if the transformer is 225kVA, it can have 200kW, 150kW, 100kW, 50kW , 20kW, etc. Depending on the load power factor, if the load has a power of 180kVA / 144kW, it means that the power factor of this is 0.8, according to the formula of kVA to kW.
The following conversion table is available for commercial values of three-phase transformers and for power factors equal to 0.8:
| kVA | kW |
| 3 | 2.4 |
| 6 | 4.8 |
| 9 | 7.2 |
| 15 | 12 |
| 30 | 24 |
| 45 | 36 |
| 75 | 60 |
| 112.5 | 90 |
| 150 | 120 |
| 225 | 180 |
| 300 | 240 |
| 500 | 400 |
| 750 | 600 |
| 800 | 640 |
| 1000 | 800 |
| 1250 | 1000 |
| 1600 | 1280 |
| 2000 | 1600 |
| 2500 | 2000 |
| 3000 | 2400 |
| 3750 | 3000 |
KVA to kW table for single phase transformers (power factor of 0.8):
| kVA | kW |
| 0.25 | 0.2 |
| 0.5 | 0.4 |
| 0.75 | 0.6 |
| 1 | 0.8 |
| 1.5 | 1.2 |
| 2 | 1.6 |
| 3 | 2.4 |
| 5 | 4 |
| 7.5 | 6 |
| 10 | 8 |
| 15 | 12 |
| 25 | 20 |
| 37.5 | 30 |
| 50 | 40 |
| 75 | 60 |
| 100 | 80 |
| 167 | 133.6 |
| 250 | 200 |
| 333 | 266.4 |
KVA to kW table for generators (power factor of 0.8):
Unlike the transformers, the kVA of the generators cannot have many equivalences in kW, which means that if a generator is 225kVA it can have an equivalence of up to 180kW or a little less but it cannot have as many equivalence of kVA to kW as a transformer, this is because the generator has a greater power factor limitation than a transformer (Commonly the minimum power factor of the generators is 0.8).
In addition to the above, the power of a generator depends on: The elevation of the installation, the temperature, the quality of the fuel, the age, the size and other factors can reduce the amount of energy that can be generated in a specific installation.
Some commercial values of generators with power factors equal to 0.8 have the following table of kVA to kW:
| kVA | kW |
| 3 | 2.4 |
| 6 | 4.8 |
| 6.3 | 5.04 |
| 9.4 | 7.52 |
| 10 | 8 |
| 12 | 9.6 |
| 12.5 | 10 |
| 15 | 12 |
| 18 | 14.4 |
| 18.7 | 14.96 |
| 20 | 16 |
| 25 | 20 |
| 26 | 20.8 |
| 30 | 24 |
| 31.3 | 25.04 |
| 37.5 | 30 |
| 45 | 36 |
| 50 | 40 |
| 60 | 48 |
| 62.5 | 50 |
| 75 | 60 |
| 90 | 72 |
| 93.8 | 75.04 |
| 100 | 80 |
| 120 | 96 |
| 125 | 100 |
| 150 | 120 |
| 156 | 124.8 |
| 175 | 140 |
| 187 | 149.6 |
| 200 | 160 |
| 219 | 175.2 |
| 250 | 200 |
| 312 | 249.6 |
| 375 | 300 |
| 438 | 350.4 |
| 500 | 400 |
| 625 | 500 |
| 750 | 600 |
| 875 | 700 |
| 1000 | 800 |
| 1125 | 900 |
| 1250 | 1000 |
| 1563 | 1250.4 |
| 1875 | 1500 |
| 2188 | 1750.4 |
| 2500 | 2000 |
| 2812 | 2249.6 |
| 3125 | 2500 |
| 3750 | 3000 |
| 4375 | 3500 |
| 5000 | 4000 |
KVA to kW table for UPS (Power Factor of 0.8):
In many uninterruptible power supplies below 2 kVA, it is common to find a power factor of less than 1.0 and, in many cases, as low as 0.6 for smaller systems.
This allows UPS manufacturers to offer a 0.3kW UPS that can deliver 0.5kVA which apparently shows a much more robust equipment than it actually is. This practice is less and less common, which is why it is so important to check the kW and KVA of a UPS.
This becomes even more important as the loads increase in size. Larger UPSs tend to be rated with a higher output power factor of at least 0.9. Legacy systems can be found around 0.8 and the latest uninterruptible power supplies tend to be launched with 1 output standards where the same UPS will deliver similar kW and kVA values.
This table shows the commercial values of some UPS with power factors equal to 0.8:
| kVA | kW |
| 2.5 | 2 |
| 3 | 2.4 |
| 3.5 | 2.8 |
| 4 | 3.2 |
| 4,5 | 3.6 |
| 5 | 4 |
| 5.5 | 4.4 |
| 6 | 4.8 |
| 6.5 | 5.2 |
| 7 | 5.6 |
| 7.5 | 6 |
| 8 | 6.4 |
| 8.5 | 6.8 |
| 9 | 7.2 |
| 9.5 | 7.6 |
| 10 | 8 |
| 10.5 | 8.4 |
| 11 | 8.8 |
| 11.5 | 9.2 |
| 12 | 9.6 |
| 12.5 | 10 |
| 13 | 10.4 |
| 13.5 | 10.8 |
| 14 | 11.2 |
| 14.5 | 11.6 |
| 15 | 12 |
| 20 | 16 |
| 30 | 24 |
| 40 | 32 |
| fifty | 40 |
| 60 | 48 |
| 80 | 64 |
| 100 | 80 |
| 120 | 96 |
| 160 | 128 |
| 275 | 220 |
| 550 | 440 |
| 650 | 520 |
| 750 | 600 |
| 825 | 660 |
| 1000 | 800 |
| 1100 | 880 |
🔥Relationship and difference between kVA, kW and Fp .
The main difference between kW (kilowatts) and kVA (kilovolts-amps) is the power factor . kW is the unit of real power and kVA is a unit of apparent power (or real power plus reactive power). The power factor, unless defined and known, is therefore an approximate value (typically 0.8) , and the value of kVA will always be greater than the value for kW.
The so-called Power Factor is a nebulous value that can vary for each electrical device or device. In essence, the value of the Power Factor is given in a percentage, or from 0 to 1 , where 100 percent is 1 and is considered unit. The closer the power factor of the unit is, the more efficient a particular device will be with the use of electricity
In DC direct current circuits , kVA is equal to kW , since the power factor in these DC equipment is equal to 1. However, the “apparent power” and “real power” may differ in the alternating current circuits .
An example that is commonly used to explain the difference between kVA vs kW is beer . The total content of a glass of beer (liquid + foam) is the kVA . However, only the liquid part of your beer serves to quench your thirst, this would be the equivalent of kW , while the foam would be the kVAR , and in total liquid more foam would be the kVA . The better the beer is served (the more efficient the electrical system), the less foam (kVAR) will be made in the glass and the more liquid (kW) will be obtained.
In conclusion, the more kW the more efficient the electrical system .
Difference between kVA vs kW.
In other words, the kVA cannot be without the kW but the latter can be without the kVA, which indicates that in alternating current (AC) there are kVA and kW while in direct current (DC) there are only kW , This occurs because in AC there is the power factor (FP), while in direct current there is no FP or it is equal to 1.
From the above we can deduce that the difference between kVA and kW is the famous power factor that depending on the current (AC or DC) and the electrical equipment fluctuates between Zero (0) and one (1).
Now if we replace in the formula the value of power factor equal to 1, we can realize that the kW are converted to kVA (KW = kVAx1), the value of 1 is only given in DC circuits and purely resistive loads (AC) In reality, the latter are not common because all real AC loads have some inductive.
It should be kept in mind that it is the same formula for single-phase, two-phase and three-phase systems.
👌Definitions of kVA, kW and FP:
kVA, commonly called apparent power and designated with the letter “S”.
The power in kVA is the total power of an inductive system or equipment , what does this mean ?, that the power in kVA will only be present in equipment that has components that require some type of induction , such as: motors, generators, transformers etc.
Being a little more technical we can say that the kVA are produced when the voltage and current are not in phase , therefore the KVA will be different from the KW, this only happens when the voltage and current are out of phase, it must be keep in mind that KVA will always be higher than KW , this leads to another question that is then kW ?.
kW, This power is called real power and is designated with the letter “P”.
Is the power that really does the job and is present in all electrical equipment whether inductive or resistive, which means ?, that this power is used in all electrical appliances regardless of whether they have motors, resistors, electronics, etc. to perform the heating, lighting, movement, pumping, etc. This power is always less than kVA. The last question then arises which is the power factor and how does it relate to the kVA and kW ?
Power factor, the power factor defines how efficiently electricity is used.
Which indicates the total power in kVA how much is actually used in kW.
The power factor is the ratio (phase) of the current and voltage in AC electrical distribution systems . Under ideal conditions, the current and voltage are “in phase” and the power factor is “100%”. If there are inductive loads (motors), a power factor of less than 100% (typically 80 to 90%) may occur . Some typical power factor values for equipment are presented in this table .
The low power factor, electrically speaking , causes a greater current to flow in the power distribution lines to deliver a given number of kilowatts to an electric load.
⭐Common conversions (monophasic, biphasic and three-phase):
What is the equivalence of 12kVA to kW?
The quick response is 9.6kW, taking into account a power factor of 0.8, which is a common power factor in electrical equipment, however to know exactly the value of this equivalence you must have the power factor exact equipment.
How much is 1 kVA to kW?
Using the formula the result is 0.8kW, this value can only be applied to equipment that has a power factor value of 0.8.
350kVA to kW transformation:
As long as the power factor is 0.8, 350kVA equals 280kW.
How much is 10kVA to kW:
This value is commonly used for UPS and the equivalence is 8kW, with a fp = 0.8, if the equipment is more efficient, a higher power factor such as 0.9 could be used, which would give a value of 0.8kW.
80kVA at kW:
If the formula is used, with a power factor of 0.8, the equivalence is 64kW