Understanding a circle’s radius is essential in geometry, engineering, physics, mathematics, design, architecture, and computer graphics. This guide explores technical methods for calculating, applying, and analyzing radius, including formulas, examples, and applications.
Circle Radius Calculator
How is the radius calculated?
What if I only know circumference or diameter?
Circle Radius: Fundamental Concepts
The radius of a circle is the distance from the center of the circle to any point on its circumference. It is a crucial parameter in defining the size and properties of a circle. The relationship between the radius and other circle properties is governed by several key formulas:
- Circumference (C):

- Area (A):

- Diameter (D): The distance across the circle through its center.

These formulas are interrelated, and knowing one property allows for the calculation of the others.
Common Radius Values and Their Applications
In various practical scenarios, certain radius values are frequently encountered. Below is a table showcasing these common values along with their corresponding circumference, area, and diameter.
| Radius (r) | Circumference (C) | Area (A) | Diameter (D) |
|---|---|---|---|
| 1 unit | 6.2832 units | 3.1416 sq. units | 2 units |
| 5 units | 31.4159 units | 78.5398 sq. units | 10 units |
| 10 units | 62.8318 units | 314.1593 sq. units | 20 units |
| 50 units | 314.1593 units | 7853.9816 sq. units | 100 units |
| 100 units | 628.3185 units | 31415.9265 sq. units | 200 units |
These values are commonly used in fields such as architecture, manufacturing, and design, where standard measurements are essential.
Deriving the Radius from Other Circle Properties
While the radius is often given, there are situations where it must be calculated from other known properties. The following formulas are used to derive the radius from the circumference, area, and diameter:

These formulas are essential when only partial information is available, allowing for the determination of the radius.
Real-World Applications of Circle Radius Calculations
1. Designing a Circular Garden
Consider a landscape architect tasked with designing a circular garden with a radius of 7 meters. To determine the amount of fencing required (circumference) and the area to be planted, the following calculations are made:
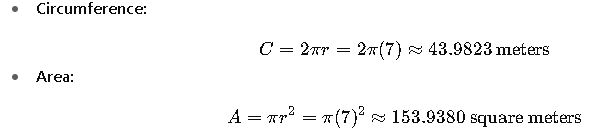
These calculations help in estimating the materials needed for fencing and the quantity of soil required for planting.
2. Manufacturing a Circular Metal Plate
A manufacturer needs to produce a circular metal plate with a radius of 0.5 meters. To calculate the amount of material required, the area is determined:
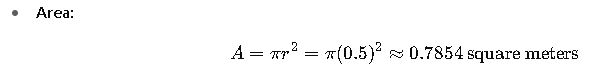
This information is crucial for estimating material costs and production time.
Advanced Considerations in Circle Radius Calculations
In more complex scenarios, additional factors may influence radius calculations:
- Variable Radius: In some applications, the radius may change along the circumference, requiring integration to calculate the area or circumference.
- Sector and Segment Areas: When dealing with portions of a circle, formulas for sector and segment areas are used:

These formulas are particularly useful in fields such as astronomy, engineering, and architecture.
Conclusion
Understanding the radius of a circle and its associated properties is fundamental in various technical fields. By mastering the formulas and applications discussed in this guide, professionals can accurately perform calculations and make informed decisions in their respective domains.
For further reading and tools related to circle calculations, consider exploring the following resources:
- Calculator.net Circle Calculator
- Omni Calculator: Circle Radius
- Math Open Reference: Radius of a Circle
These resources provide interactive tools and additional information to enhance your understanding of circle radius calculations.