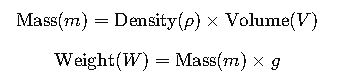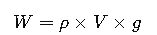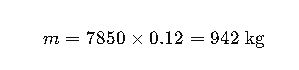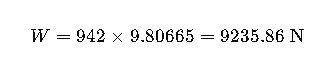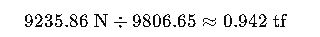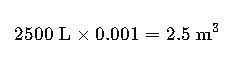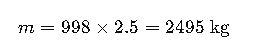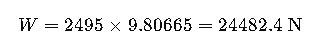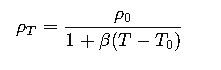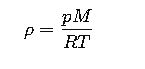The calculation of weight from volume and density is fundamental in engineering, physics, and logistics.
It enables accurate estimation of mass and weight, optimizing transport, manufacturing, and storage operations.
Weight Calculator (kg) from Volume and Density
What formula is used?
Unit conversions are applied: 1 m³ = 1000 L = 1,000,000 cm³; 1 g/cm³ = 1000 kg/m³.
Which units should I use?
Core Formulas for Calculating Weight from Volume and Density
There are two main approaches:
- The two-step method, where mass is calculated first.
- The direct method, where weight is obtained in a single step.
1. Two-Step Method (Standard Approach)
Where:
- ρ(Density): The amount of mass per unit volume.
- SI Unit: kg/m³
- Common values:
- Water: 1000 kg/m³
- Steel: 7850 kg/m³
- Air (20°C): 1.204 kg/m³
- V(Volume): The space occupied by the object or substance.
- SI Unit: m³
- Conversion: 1 liter = 0.001 m³
- m(Mass): Amount of matter in an object.
- SI Unit: kg
- g(Acceleration due to gravity): Intensity of gravitational attraction.
- Standard Earth value: 9.80665 m/s² (ISO 80000-3).
- W(Weight): The force of gravity acting on a mass.
- SI Unit: Newton (N).
2. Direct Method (Integrating Gravity)
This formula allows direct calculation of weight from density and volume without computing mass separately.
Common Density Values Table
The following table lists densities of common materials and substances under standard conditions (approximately 20 °C and 1 atm), useful for quick calculations.
| Material / Substance | Density (kg/m³) | Notes & Conditions |
|---|---|---|
| Pure water | 1000 | At 4°C, max density |
| Seawater | 1025 | Average, depends on salinity |
| Ice | 917 | At approx. -5°C |
| Carbon steel | 7850 | Structural grade |
| Aluminum | 2700 | Common alloys |
| Copper | 8960 | High purity |
| Gold | 19300 | 24 karat |
| Lead | 11340 | Standard purity |
| Reinforced concrete | 2400 | Apparent density |
| Oak wood | 710 | 12% moisture content |
| Air | 1.204 | 20°C, 1 atm |
| Hydrogen | 0.0899 | 0°C, 1 atm |
| Gasoline | 720 | Average |
| Olive oil | 920 | 20°C |
| Soda-lime glass | 2500 | Common use |
| Polyethylene (PE) | 950 | High density |
| Cast iron | 6800 | Approximate |
| Titanium | 4500 | Commercial grade |
| Mercury | 13534 | 20°C |
| Dry sand | 1600 | Medium grain |
| Wet sand | 2000 | Saturated |
| Dry clay | 1700 | Apparent density |
| Wet clay | 2100 | Saturated |
Common Unit Conversions
In practice, data is often provided in non-SI units. Knowing how to convert them is essential:
| Quantity | Common Unit | Equivalent in SI Units |
|---|---|---|
| Volume | Liter (L) | 1 L = 0.001 m³ |
| Volume | US gallon | 1 gal (US) = 0.00378541 m³ |
| Volume | Cubic inch | 1 in³ = 1.6387 × 10⁻⁵ m³ |
| Mass | Pound (lb) | 1 lb = 0.45359237 kg |
| Mass | Metric ton | 1 t = 1000 kg |
| Weight | Pound-force (lbf) | 1 lbf = 4.44822 N |
Real-World Example 1: Steel Beam Weight Calculation
Given:
- Steel type: structural, density ρ=7850 kg/m3
- Beam volume: 0.12 m3
- Gravity: g=9.80665 m/s2
Step 1 — Mass:
Step 2 — Weight:
Step 3 — Convert to metric tons-force:
Result: The beam weighs approximately 9236 N or 0.94 metric tons-force.
Real-World Example 2: Water Tank Weight Calculation
Given:
- Water at 20°C: ρ=998 kg/m3
- Capacity: 2500 L
- Gravity: standard
Volume conversion:
Mass:
Weight:
Result: The full tank weighs 24.48 kN, equivalent to ~2.5 metric tons-force.
Applications Across Industries
The calculation of weight from volume and density is applied in:
- Civil engineering: structural load design, permanent load estimation (Eurocode EN 1991)
- Logistics & transportation: determining cargo mass for maritime and air freight
- Chemical industry: dosing solids and liquids accurately
- Aerospace & naval engineering: stability and balance of mass distributions
- Mechanical construction: sizing cranes, hoists, and supports
Extended Density Tables for Engineering Applications
While the previous table covered common everyday materials, professionals often require density data for industrial gases, specialized liquids, alloys, and rare metals. Below are extended datasets suitable for engineering calculations.
Density of Industrial and Specialty Liquids (20°C, 1 atm)
| Substance | Density (kg/m³) | Notes / Typical Use |
|---|---|---|
| Ethanol | 789 | Solvent, biofuel |
| Methanol | 792 | Chemical feedstock |
| Glycerin | 1260 | Pharmaceutical & cosmetic |
| Acetone | 784 | Solvent |
| Sulfuric acid (98%) | 1840 | Industrial chemical |
| Sodium hydroxide (50%) | 1530 | Chemical processing |
| Diesel fuel | 830 | Automotive fuel |
| Jet A-1 fuel | 804 | Aviation |
| Kerosene | 810 | Heating & lighting |
| Liquid nitrogen | 808 | Cryogenics (-196°C) |
| Liquid oxygen | 1140 | Cryogenics (-183°C) |
| Liquid helium | 125 | Cryogenics (-269°C) |
Density of Gases (20°C, 1 atm)
| Gas | Density (kg/m³) | Notes |
|---|---|---|
| Air | 1.204 | Average composition |
| Helium | 0.1785 | Lighter-than-air gas |
| Hydrogen | 0.0899 | Lightest element |
| Oxygen | 1.429 | Pure O₂ |
| Nitrogen | 1.2506 | Pure N₂ |
| Carbon dioxide | 1.977 | CO₂, greenhouse gas |
| Propane | 1.882 | LPG |
| Ammonia | 0.771 | NH₃, industrial gas |
| Methane | 0.656 | Natural gas |
| Sulfur hexafluoride | 6.17 | SF₆, electrical insulation |
Density of Metals and Alloys
| Metal / Alloy | Density (kg/m³) | Notes |
|---|---|---|
| Stainless steel (304) | 8000 | Corrosion resistant |
| Brass | 8500 | Cu-Zn alloy |
| Bronze | 8800 | Cu-Sn alloy |
| Nickel | 8908 | Corrosion resistant |
| Tungsten | 19300 | Very high density |
| Uranium | 18950 | Depleted uranium applications |
| Silver | 10490 | High conductivity |
| Zinc | 7135 | Coatings, galvanization |
| Magnesium | 1738 | Lightweight structural material |
Advanced Considerations: Temperature and Pressure Effects
In real-world scenarios, density is not constant—it changes with temperature and, for gases, with pressure. Failing to account for these changes can lead to significant errors.
1. Liquids
Most liquids expand when heated, decreasing their density. This change can be approximated by:
Where:
- ρT= density at temperature T
- ρ0= density at reference temperature T0
- β= volumetric thermal expansion coefficient (1/°C)
- T, T0 in °C
For water, β≈0.00021 °C−1
2. Gases
For ideal gases, density is calculated using the Ideal Gas Law:
Where:
- p= absolute pressure (Pa)
- M= molar mass (kg/mol)
- R= universal gas constant (8.314462618 J/mol·K)
- T= absolute temperature (K)
This means that doubling the temperature (in Kelvin) halves the density, if pressure is constant.
Reverse Calculations
Sometimes we need the opposite:
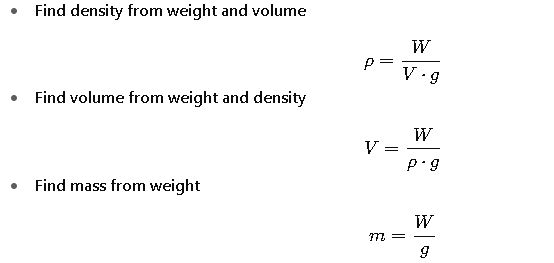
Real-World Example 3: Cargo Ship Load Calculation with Seawater Density
Scenario: A cargo ship is designed to carry 150,000 m³ of crude oil. We need to know the weight of the load in kilonewtons (kN) when density is 870 kg/m³.
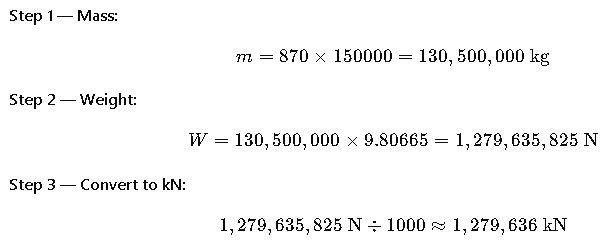
Result: The crude oil weighs approximately 1.28 million kN.
Real-World Example 4: Gas Cylinder Content Weight
Scenario: An industrial oxygen cylinder contains 40 m³ of gas at 1 atm and 20°C. Oxygen density at these conditions is 1.429 kg/m³.
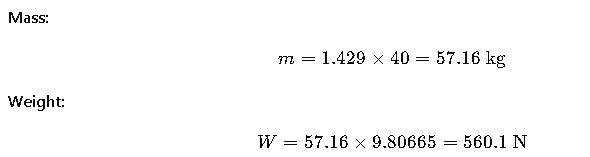
Result: The gas inside weighs about 560 N (~57 kg mass).
Common Mistakes and Best Practices
Mistakes:
- Mixing units — using liters for volume and kg/m³ for density without conversion.
- Ignoring temperature effects — especially in gases, density varies greatly with temperature.
- Confusing mass with weight — mass is in kg, weight is a force in N.
- Using approximate gravity values — for precision, use 9.80665 m/s².
Best Practices:
- Always convert to SI units before calculation.
- For high accuracy, use density values at the exact temperature and pressure.
- Reference authoritative standards:
- ISO 80000-4 for quantities and units.
- ASTM D1250 for petroleum liquid densities.