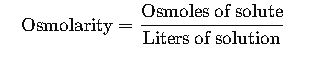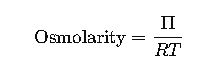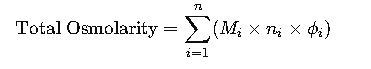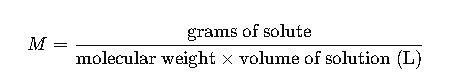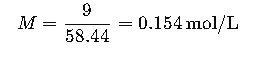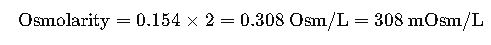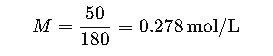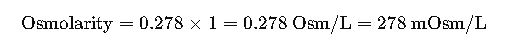Osmolarity is fundamental in chemistry, biology, and medicine, regulating water movement and influencing cellular equilibrium. Precise osmolarity calculations are vital for researchers, clinicians, pharmacists, and engineers managing biological and industrial systems.
Osmolarity Calculator — Osmol/L & mOsm/L
What is osmolarity?
Formulas used
Convert volume to liters when needed.
Molarity (C) = moles / volume (L).
Osmolarity = i · C where i is Van’t Hoff factor (particles per formula unit).
Fundamental Definition
Osmolarity is defined as the number of osmoles of solute per liter of solution:
Where:
- Osmole (Osm) represents the amount of a substance that dissociates in solution to form one mole of osmotically active particles.
- Units: Osm/L (commonly expressed as mOsm/L).
This distinguishes osmolarity from molarity, which only accounts for the concentration of solute molecules, not their dissociation into ions.
Core Formulas for Osmolarity
1. General Formula

2. Van ’t Hoff Equation for Osmotic Pressure (related concept)

This formula is essential because osmotic pressure is directly proportional to osmolarity:
3. Practical Osmolarity for Solutions with Multiple Solutes
For clinical and laboratory solutions containing more than one solute:
This summation accounts for glucose, electrolytes, urea, and other solutes simultaneously present.
Extended Reference Table of Common Compounds and Their Osmolarity Factors
The following table summarizes the most common solutes encountered in laboratories, medicine, and chemistry. It includes their dissociation number nnn, typical molarity ranges, and approximate osmolarities.
Note: Osmotic coefficients (ϕ) are assumed close to 1 unless otherwise specified. Values are representative and can vary with temperature and ionic strength.
| Compound | Formula | Dissociation Factor (n) | Example Concentration (M) | Approx. Osmolarity (mOsm/L) |
|---|---|---|---|---|
| Sodium chloride | NaCl | 2 | 0.154 M (0.9% saline) | 308 mOsm/L |
| Potassium chloride | KCl | 2 | 0.10 M | 200 mOsm/L |
| Calcium chloride | CaCl2_22 | 3 | 0.10 M | 300 mOsm/L |
| Magnesium sulfate | MgSO4_44 | 2 | 0.10 M | 200 mOsm/L |
| Glucose (dextrose) | C6_66H12_{12}12O6_66 | 1 | 0.278 M (5% w/v) | 278 mOsm/L |
| Urea | CO(NH2_22)2_22 | 1 | 0.10 M | 100 mOsm/L |
| Sucrose | C12_{12}12H22_{22}22O11_{11}11 | 1 | 0.10 M | 100 mOsm/L |
| Sodium bicarbonate | NaHCO3_33 | 2 | 0.10 M | 200 mOsm/L |
| Sodium phosphate (monobasic) | NaH2_22PO4_44 | 2 | 0.10 M | 200 mOsm/L |
| Sodium phosphate (dibasic) | Na2_22HPO4_44 | 3 | 0.10 M | 300 mOsm/L |
| Potassium phosphate (monobasic) | KH2_22PO4_44 | 2 | 0.10 M | 200 mOsm/L |
| Calcium gluconate | C12_{12}12H22_{22}22CaO14_{14}14 | 2 | 0.10 M | 200 mOsm/L |
| Mannitol | C6_66H14_{14}14O6_66 | 1 | 0.20 M | 200 mOsm/L |
This table is essential for clinical formulations, where isotonicity is required to match the osmolarity of blood plasma (~275–295 mOsm/L).
Detailed Explanation of Variables
To master osmolarity calculations, each variable must be clearly understood:
1.Molarity (M)
Defined as moles of solute per liter of solution.
Calculated by:
Common clinical molarities:
NaCl in saline: 0.154 M
Glucose in D5W: 0.278 M
2.Dissociation Factor (n)
- The number of particles produced upon dissociation:
- NaCl → Na+^++ + Cl−^-− → n=2
- CaCl2_22 → Ca2+^{2+}2+ + 2 Cl−^-− → n=3
- Glucose does not dissociate → n=1
3.Osmotic Coefficient (ϕ)
- Accounts for non-ideal ionic interactions.
- Typically 0.93–1.0 for physiological ionic strengths.
- Important in precise biochemical and pharmacological applications.
Real-World Example 1: Calculation of Osmolarity for 0.9% Normal Saline (NaCl)
Step 1. Determine molarity (M).
- 0.9 g NaCl per 100 mL = 9 g/L.
- Molecular weight of NaCl = 58.44 g/mol.
Step 2. Apply dissociation factor (n).
NaCl dissociates into 2 ions.
Result:
0.9% NaCl has an osmolarity of ~308 mOsm/L, making it nearly isotonic with plasma.
Real-World Example 2: Intravenous Dextrose 5% (D5W)
Step 1. Determine molarity (M).
- 5 g glucose per 100 mL = 50 g/L.
- Molecular weight of glucose = 180 g/mol.
Step 2. Apply dissociation factor (n).
- Glucose does not dissociate (n=1).
Result:
D5W has an osmolarity of ~278 mOsm/L, also isotonic with plasma.
Clinical Relevance of Osmolarity
Osmolarity plays a central role in medical practice, especially in intravenous (IV) therapy, dialysis, parenteral nutrition, and ophthalmology. Plasma osmolarity in humans typically ranges between 275 and 295 milliosmoles per liter. Deviations outside this range can cause severe physiological consequences.
- Hypoosmolar solutions (below 275 mOsm/L) may cause water to enter cells, leading to swelling and potential lysis. This is particularly dangerous in brain cells, where cerebral edema can be life-threatening.
- Hyperosmolar solutions (above 295 mOsm/L) draw water out of cells, causing cellular shrinkage. In clinical contexts, this can induce dehydration, neurological dysfunction, and renal stress.
- Isotonic solutions (within the plasma osmolarity range) are used for safe volume expansion without causing osmotic shifts.
For these reasons, hospitals carefully calculate osmolarity before administering IV fluids. Pharmacy standards, such as those established by the United States Pharmacopeia (USP) and World Health Organization (WHO), require precise formulation to ensure patient safety.
Common Clinical Solutions and Their Approximate Osmolarities
The following table presents widely used intravenous solutions with their approximate osmolarity values. These values are critical for both healthcare professionals and pharmacists.
| Solution Type | Composition (per liter) | Approximate Osmolarity (mOsm/L) | Clinical Use Case |
|---|---|---|---|
| 0.9% Sodium Chloride (Normal Saline) | 154 mmol NaCl | 308 | Fluid resuscitation, isotonic hydration |
| 5% Dextrose in Water (D5W) | 50 g glucose | 278 | Energy source, isotonic hydration |
| Lactated Ringer’s Solution | NaCl, KCl, CaCl2, Na lactate | 273 | Burn therapy, surgical fluid replacement |
| 3% Sodium Chloride | 513 mmol NaCl | 1026 | Treatment of severe hyponatremia |
| 10% Mannitol | 100 g mannitol | 550 | Reduction of intracranial pressure |
| 20% Glucose | 200 g glucose | 1111 | Hypertonic caloric source in parenteral nutrition |
| 8.4% Sodium Bicarbonate | 100 mmol NaHCO3 | 200 | Treatment of metabolic acidosis |
These solutions demonstrate the variety of osmolarity levels required to meet specific clinical needs, ranging from isotonic maintenance fluids to hypertonic agents for targeted therapies.
Osmolarity in Total Parenteral Nutrition (TPN)
Total parenteral nutrition is one of the most challenging areas where osmolarity calculation is essential. TPN formulations combine amino acids, dextrose, lipids, electrolytes, trace elements, and vitamins. Each component contributes to the total osmolarity of the infusion.
- Dextrose contributes significantly because of its high concentrations in central TPN solutions.
- Amino acids typically contribute 8 to 10 mOsm per gram.
- Electrolytes such as sodium, potassium, calcium, magnesium, and phosphate can dramatically increase osmolarity due to their dissociation into multiple particles.
Peripheral vein infusions must remain below 900 mOsm/L to avoid vein irritation, while central vein infusions can exceed 1800 mOsm/L. This distinction is crucial to prevent complications such as phlebitis or vascular damage.
Osmolarity in Dialysis
In hemodialysis and peritoneal dialysis, osmolarity governs the removal of waste products and excess water.
- Hemodialysis solutions are carefully balanced to match plasma osmolarity, typically around 285 mOsm/L, to avoid osmotic shifts that could destabilize blood cells.
- Peritoneal dialysis solutions often include glucose at different concentrations (1.5%, 2.5%, or 4.25%), creating a hyperosmolar environment that promotes fluid removal from the peritoneal cavity.
Precise osmolarity calculation ensures effective clearance of urea and creatinine while preventing cellular damage in patients with renal failure.
Industrial and Biotechnological Applications
Beyond medicine, osmolarity calculations are critical in food science, fermentation technology, and bioprocessing.
- Fermentation Processes
Microorganisms such as yeast and bacteria require tightly controlled osmotic environments. High sugar concentrations, for example in brewing or bioethanol production, create hyperosmotic conditions that can stress cells and slow down growth. Controlling osmolarity ensures optimal yields and prevents fermentation failures. - Cell Culture and Biotechnology
Mammalian cell cultures used in pharmaceuticals and vaccine production are highly sensitive to osmolarity. Deviations as small as 10% can impair protein expression, antibody yield, or cell viability. Bioreactors therefore monitor osmolarity in real time, adjusting feed solutions to maintain stability. - Food Preservation
Salt and sugar are traditional preservatives not only because they inhibit microbial growth through osmotic stress, but also because they adjust osmolarity to unfavorable levels for spoilage organisms. Calculating osmolarity helps optimize recipes for jams, syrups, and brines.
Osmolarity versus Osmolality
Although often used interchangeably, osmolarity and osmolality have distinct definitions.
- Osmolarity refers to osmoles per liter of solution, influenced by temperature and solution volume.
- Osmolality refers to osmoles per kilogram of solvent, independent of temperature or pressure.
Clinically, osmolality is often preferred for laboratory measurement because it is not affected by thermal expansion. However, in practical formulation and bedside calculations, osmolarity remains the most common unit because it is easier to derive from concentrations expressed in liters.
Measurement Methods
In addition to theoretical calculation, osmolarity can be measured experimentally. The two most common laboratory techniques are:
- Freezing Point Depression
A colligative property where the presence of solute lowers the freezing point of a solvent. The magnitude of depression correlates with osmolality. Instruments called osmometer devices use this principle to measure plasma or urine osmolality. - Vapor Pressure Osmometry
Based on the reduction in vapor pressure caused by solutes. Although less common in clinical laboratories, it is widely used in research settings.
These measurement methods provide direct verification of calculated osmolarity, ensuring accuracy in clinical decision-making.