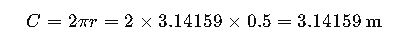Understanding circle geometry is essential across fields like engineering, architecture, physics, mathematics, and technical design. This guide explores formulas for calculating circle area and circumference, including detailed explanations, examples, applications.
Circle Area & Circumference Calculator
How is the area calculated?
How is the circumference calculated?
1. Formulas for Area and Circumference of a Circle
Area of a Circle
The area A of a circle is the amount of space enclosed within its boundary. It can be calculated using the formula:

Alternatively, if the diameter d is known:
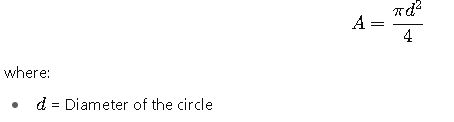
Circumference of a Circle
The circumference C of a circle is the total length around the circle. It can be calculated using the formula:

These formulas are essential for various applications, from designing circular components to calculating distances in circular paths.
2. Detailed Explanation of Variables and Common Values
Pi (π)
Pi is a mathematical constant representing the ratio of a circle’s circumference to its diameter. Its approximate value is:

Radius (r) and Diameter (d)
- Radius (r): The distance from the center of the circle to any point on its boundary.
- Diameter (d): The distance across the circle through its center, equal to twice the radius:
d=2r
Common Values
| Radius (rrr) | Diameter (ddd) | Area (AAA) | Circumference (CCC) |
|---|---|---|---|
| 1 | 2 | 3.14159 | 6.28318 |
| 2 | 4 | 12.56636 | 12.56636 |
| 3 | 6 | 28.27433 | 18.84956 |
| 5 | 10 | 78.53982 | 31.41593 |
| 10 | 20 | 314.15927 | 62.83185 |
These values are commonly used in various calculations and practical applications.
3. Real-World Applications and Examples
Example 1: Designing a Circular Garden
Suppose you are designing a circular garden with a radius of 7 meters. To calculate the area and circumference:

These calculations help in determining the amount of soil needed and the length of fencing required.
Example 2: Calculating the Distance Traveled by a Wheel
If a wheel has a radius of 0.5 meters, the distance it covers in one full rotation (its circumference) is:
This information is crucial in machinery design and transportation planning.
4. Advanced Calculations and Considerations
Calculating Area from Circumference
If the circumference C is known, the radius can be found using:

Calculating Circumference from Area
If the area A is known, the radius can be found using:

These formulas are particularly useful in reverse engineering and quality control processes.
5. Practical Applications in Various Fields
Engineering
In engineering, precise calculations of area and circumference are essential for designing components such as gears, pulleys, and wheels. For instance, the dimensions of a gear are determined based on the radius and number of teeth, which are related to the circumference.
Architecture
Architects use these calculations to design circular structures like domes and arches. The area helps in determining the material requirements, while the circumference is used for layout planning.
Physics
In physics, the motion of objects along circular paths involves calculations of distance traveled, which are based on the circumference. Additionally, the area is used in calculating moments of inertia for rotating bodies.
6. Conclusion
Understanding the formulas for the area and circumference of a circle is fundamental in various scientific and practical applications. Mastery of these calculations enables professionals to design, analyze, and optimize circular components and structures effectively.