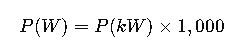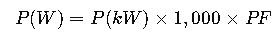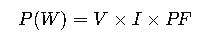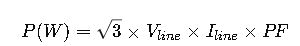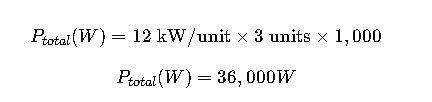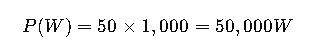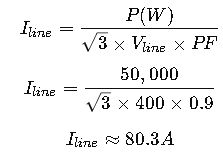Understanding the conversion between kilowatts (kW) and watts (W) is essential in electrical engineering. It is also critical for energy management, renewable systems, and includes practical examples and formulas.
kW ↔ W Calculator
Convert between kilowatts and watts instantly. Includes options for rounding and copy/share — responsive and accessible.
How does this calculator work?
What is kW used for?
Formula
W → kW: kW = W ÷ 1000.
Rounding & formatting
Kilowatts to Watts Conversion Table
To facilitate quick reference, here is an extensive table converting kilowatts to watts:
| Kilowatts (kW) | Watts (W) |
|---|---|
| 0.001 | 1 |
| 0.01 | 10 |
| 0.1 | 100 |
| 1 | 1,000 |
| 2 | 2,000 |
| 5 | 5,000 |
| 10 | 10,000 |
| 50 | 50,000 |
| 100 | 100,000 |
| 500 | 500,000 |
| 1,000 | 1,000,000 |
This table illustrates the direct proportionality between kilowatts and watts, where 1 kW equals 1,000 W.
Conversion Formula and Variable Explanation
The formula to convert kilowatts to watts is straightforward:
P(W) = P(kW) × 1,000
Where:
- P(W) is the power in watts.
- P(kW) is the power in kilowatts.
This conversion is essential when dealing with electrical systems, as watts are commonly used to specify the power consumption or generation capacity of devices and systems.
Real-World Applications and Examples
Example 1: Residential Solar Panel System
Consider a residential solar panel system rated at 5 kW. To determine its power output in watts:
P(W) = 5 kW × 1,000 = 5,000 W
This means the system can generate 5,000 watts of power under optimal conditions.
Example 2: Electric Vehicle Charging Station
An electric vehicle charging station has a power output of 22 kW. To convert this to watts:
P(W) = 22 kW × 1,000 = 22,000 W
This indicates the charging station can deliver 22,000 watts of power to charge vehicles.
Extended Conversion Tables for Common kW Values
For professionals working with electrical installations, having extended reference tables simplifies calculations without constant formula use. Here is a more comprehensive kW to Watts table including fractional and larger values:
| Kilowatts (kW) | Watts (W) |
|---|---|
| 0.001 | 1 |
| 0.005 | 5 |
| 0.01 | 10 |
| 0.05 | 50 |
| 0.1 | 100 |
| 0.15 | 150 |
| 0.2 | 200 |
| 0.25 | 250 |
| 0.5 | 500 |
| 1 | 1,000 |
| 1.5 | 1,500 |
| 2 | 2,000 |
| 2.5 | 2,500 |
| 3 | 3,000 |
| 5 | 5,000 |
| 7.5 | 7,500 |
| 10 | 10,000 |
| 15 | 15,000 |
| 20 | 20,000 |
| 25 | 25,000 |
| 50 | 50,000 |
| 75 | 75,000 |
| 100 | 100,000 |
| 200 | 200,000 |
| 500 | 500,000 |
| 1,000 | 1,000,000 |
| 1,500 | 1,500,000 |
| 2,000 | 2,000,000 |
| 5,000 | 5,000,000 |
This table covers both small household appliances and large industrial machines, making it invaluable for engineers, electricians, and energy managers.
Detailed Formula Analysis and Variable Explanation
The basic formula remains:
However, in advanced applications, several factors may influence the calculation:
1.Power Factor (PF) – In AC circuits, real power differs from apparent power.
PF ranges from 0 to 1.
Residential loads: typically 0.8–1.
Industrial motors: often 0.85–0.95.
Correcting for PF ensures accurate real power calculations.
2.Voltage and Current Considerations – Sometimes engineers need to back-calculate power from voltage and current:
- V = Voltage in volts.
- I = Current in amperes.
- This is particularly useful for sizing circuits and breakers.
3.Three-Phase Systems – Industrial settings often use three-phase power:
- V_line = Line-to-line voltage.
- I_line = Line current.
- √3 accounts for phase relationships in three-phase circuits.
These extended formulas allow professionals to transition from simple kW-to-W conversions to complete system design calculations.
Real-World Case Studies
Case Study 1: Office Building Energy Assessment
Scenario:
An office building uses HVAC units rated at 12 kW each, with three units running simultaneously. The facility manager wants to know total power in watts.
Calculation:
Interpretation:
The office’s HVAC system consumes 36,000 watts when operating at full capacity. This informs electrical panel sizing, load balancing, and energy billing.
Case Study 2: Industrial Motor Sizing
Scenario:
A factory installs a three-phase motor rated 50 kW with a power factor of 0.9. Line voltage is 400 V. Determine the line current.
Step 1: Convert kW to W
Step 2: Apply three-phase formula
Result:
The motor draws approximately 80.3 amperes per line. This ensures the wiring, breakers, and protection devices are appropriately rated.
Best Practices for Using kW to Watts Conversion
- Always check if you need real power (W) or apparent power (VA).
- Include power factor in AC system calculations to avoid undersizing equipment.
- Use conversion tables for quick reference in design and field work.
- For large systems, consider harmonics and efficiency impacts on actual power usage.
- Validate calculations against national standards (NEC, IEC, IEEE).