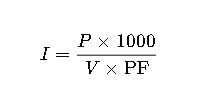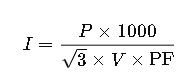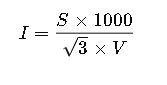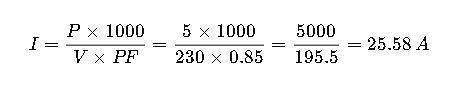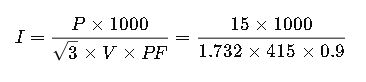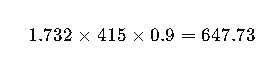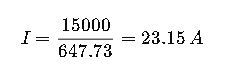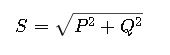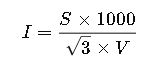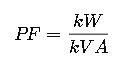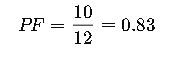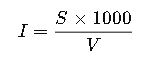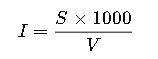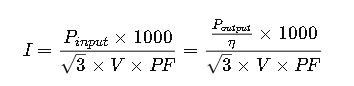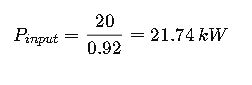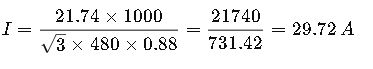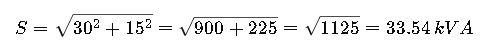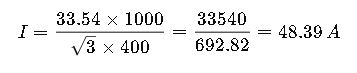Accurate kW to Amps conversion is vital in engineering design, equipment selection, and safety compliance.
This calculator includes formulas, detailed tables, and real-world examples to determine current from known power.
kW ↔ A Calculator
Extensive Tables of Common kW to Amps Conversions
The conversion of kW to Amps depends heavily on the voltage, phase type (single-phase, three-phase), and power factor (PF) of the load. The following tables summarize the most common conversions based on these parameters, widely used in industry.
Table 1: Single-Phase Systems (Voltage = 120 V, 230 V, 240 V)
| Power (kW) | Voltage (V) | Power Factor (PF) | Current (A) |
|---|---|---|---|
| 1 | 120 | 1.0 | 8.33 |
| 1 | 230 | 1.0 | 4.35 |
| 1 | 240 | 1.0 | 4.17 |
| 5 | 120 | 0.85 | 49.02 |
| 5 | 230 | 0.85 | 25.40 |
| 5 | 240 | 0.85 | 24.51 |
| 10 | 120 | 0.9 | 92.59 |
| 10 | 230 | 0.9 | 48.02 |
| 10 | 240 | 0.9 | 46.30 |
| 15 | 120 | 0.8 | 156.25 |
| 15 | 230 | 0.8 | 81.52 |
| 15 | 240 | 0.8 | 78.13 |
Table 2: Three-Phase Systems (Voltage = 400 V, 415 V, 480 V)
| Power (kW) | Voltage (V) | Power Factor (PF) | Current (A) |
|---|---|---|---|
| 1 | 400 | 1.0 | 1.44 |
| 1 | 415 | 1.0 | 1.39 |
| 1 | 480 | 1.0 | 1.20 |
| 5 | 400 | 0.9 | 8.01 |
| 5 | 415 | 0.9 | 7.72 |
| 5 | 480 | 0.9 | 6.01 |
| 10 | 400 | 0.85 | 17.95 |
| 10 | 415 | 0.85 | 17.31 |
| 10 | 480 | 0.85 | 13.41 |
| 20 | 400 | 0.8 | 36.06 |
| 20 | 415 | 0.8 | 34.73 |
| 20 | 480 | 0.8 | 26.04 |
Table 3: Common Power Factor Values in Industry
| Equipment Type | Typical Power Factor (PF) |
|---|---|
| Resistive Loads (Heaters, Incandescent lamps) | 1.0 (unity) |
| Motors (Industrial AC motors) | 0.8 – 0.9 |
| Fluorescent Lighting | 0.7 – 0.9 |
| Computer Equipment, Electronics | 0.6 – 0.9 |
| Variable Frequency Drives | 0.7 – 0.95 |
Detailed Formulas for kW to Amps Conversion
The formulas to convert power in kilowatts (kW) to current in amperes (A) depend on system configuration: single-phase or three-phase, voltage, and power factor.
1. Single-Phase System
Formula:
Where:
- I= Current in amperes (A)
- P= Power in kilowatts (kW)
- V= Voltage in volts (V)
- PF= Power factor (unitless, between 0 and 1)
2. Three-Phase System
For three-phase systems, the current formula accounts for the square root of 3 (3≈1.732\sqrt{3} \approx 1.7323≈1.732) due to phase relationships:
Where:
- I= Current in amperes (A)
- P= Power in kilowatts (kW)
- V= Line-to-line voltage in volts (V)
- PF= Power factor (unitless)
3. Explanation of Variables and Typical Values
- Power (P): The real power consumed by the load, expressed in kilowatts (kW). 1 kW = 1000 watts (W).
- Voltage (V): The RMS voltage supplied to the load. Typical voltages vary widely:
- Residential single-phase: 120 V, 230 V, 240 V
- Industrial three-phase: 400 V, 415 V, 480 V
- Power Factor (PF): The cosine of the phase angle between voltage and current, representing efficiency of power usage.
- Values range from 0 (purely reactive) to 1 (purely resistive).
- Typical industrial loads have PF between 0.7 and 0.95.
- Current (I): The RMS current drawn by the load in amperes.
Additional Considerations:
- The formulas assume balanced loads.
- The voltage used for three-phase calculation is line-to-line voltage, not phase voltage.
- If only apparent power S (in kVA) is known, current can be calculated without PF:
Real-World Examples with Detailed Calculations
Example 1: Calculating Current for a Single-Phase Motor
Scenario:
An industrial single-phase motor rated at 5 kW operates at 230 V with a power factor of 0.85. Calculate the current drawn by the motor.
Given:
- P=5 kWP
- V=230 V
- =0.85
Calculation:
Interpretation:
The motor will draw approximately 25.58 A from the power supply.
Example 2: Calculating Current for a Three-Phase Compressor
Scenario:
A three-phase air compressor consumes 15 kW of power. The line-to-line voltage is 415 V and the power factor is 0.9. Determine the line current.
Given:
- P=15 kW
- V=415 V
- PF=0.9
Calculation:
Calculate denominator:
Calculate current:
Interpretation:
The compressor draws approximately 23.15 A on each phase.
Expanded Explanation of Examples
- In Example 1, the motor is a typical resistive-inductive load with PF less than unity, so the current is higher than if PF were 1.
- In Example 2, the three-phase formula accounts for phase differences, resulting in a lower current per phase than if it were a single-phase system at equivalent power.
Additional Important Concepts for Accurate kW to Amps Calculation
Power Factor Correction
Power factor correction (PFC) improves the PF to approach unity, reducing current for the same power output, thus improving efficiency and reducing losses.
Voltage Variations
Voltage fluctuations affect the current drawn. The formulas assume nominal voltage; deviations require recalculation.
Load Types and Their Influence
- Resistive loads have PF ≈ 1
- Inductive loads (motors, transformers) have PF < 1
- Capacitive loads can cause leading PF, affecting current calculations
Frequently Used Units and Their Conversion Factors
| Quantity | Unit | Conversion Factor |
|---|---|---|
| Power | kW | 1 kW = 1000 watts (W) |
| Voltage | Volts (V) | RMS voltage |
| Current | Amperes (A) | RMS current |
| Apparent Power | kVA | kVA = kW / PF |
| Power Factor (PF) | Unitless | Ratio, typically 0 to 1 |
Authoritative References and Standards
- IEEE Std 141-1993 — IEEE Recommended Practice for Electric Power Distribution for Industrial Plants
- IEC 60364 — Electrical Installations of Buildings (International Electrotechnical Commission)
- NFPA 70 (NEC) — National Electrical Code for wiring and safety standards
These standards provide detailed guidance on power calculation, safety margins, and electrical installation design.
Summary of Best Practices for Using kW to Amps Calculators
- Always verify voltage and phase type before calculation.
- Use the correct power factor for load type; when unknown, estimate conservatively.
- Account for continuous vs. peak loads, adding safety margins as per local regulations.
- Utilize manufacturer data sheets for exact power and current ratings.
- Consider harmonics and non-linear loads, which can affect current measurements.
Advanced Formulas and Considerations for kW to Amps Calculation
Beyond the basic formulas, engineers often need to consider specific conditions such as:
1. Apparent Power (S) and Reactive Power (Q)
In AC circuits, total power includes real power (P) and reactive power (Q):
Where:
- S= Apparent power (kVA)
- P= Real power (kW)
- Q= Reactive power (kVAR)
Current can be calculated from apparent power:
Reactive power is caused by inductive or capacitive loads and does not perform useful work but affects current.
2. Calculating Power Factor from kW and kVA
If you know kW and kVA, PF can be calculated as:
Example:
- P=10 kWP
- S=12 kVAS
3. Single-Phase Apparent Power Current
For single-phase systems, current based on apparent power is:
Where:
- S= apparent power in kVA
- V = RMS voltage (V)
4. Inclusion of Efficiency (η)
When calculating motor currents, efficiency influences input power:
Where:

Thus:
Extended Real-World Examples with Efficiency and Reactive Power
Example 3: Motor Current Including Efficiency
Scenario:
An industrial 20 kW three-phase motor has an efficiency of 92% and a power factor of 0.88. The supply voltage is 480 V. Calculate the line current.
Given:
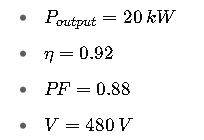
Calculate input power:
Calculate current:
Example 4: Apparent Power and Current with Known Reactive Power
Scenario:
A three-phase load consumes 30 kW and has a reactive power of 15 kVAR at 400 V. Calculate apparent power and current.
Step 1: Calculate apparent power
Step 2: Calculate current
Power Factor Impact on kW to Amps Conversion
Power factor heavily influences the current magnitude drawn by a load:
- At PF = 1, current is minimized for a given kW.
- At PF < 1, current increases proportionally (inverse relationship).
- Accurate PF measurement or estimation is critical for precise current calculations.
Typical Voltage and Power Factor Values by Region and Application
| Region/Application | Typical Voltage (V) | Typical PF Range |
|---|---|---|
| North American Residential | 120 / 240 | 0.95 – 1.0 |
| European Residential | 230 | 0.95 – 1.0 |
| Industrial (Europe, Asia) | 400 / 415 | 0.85 – 0.95 |
| Industrial (North America) | 480 | 0.85 – 0.95 |
Practical Tips for Engineers Using kW to Amps Calculators
- Always verify supply voltage and phase before calculation.
- Check power factor from manufacturer datasheets or measurements.
- Use corrected power (including efficiency) for motor applications.
- Consider starting current surges — motors can draw 6-7 times rated current during start-up.
- Apply local codes and standards for safety margins.
Online and Software kW to Amps Calculators
Many engineering software and websites offer customizable kW to Amps calculators that allow users to:
- Select voltage and phase type
- Input power factor and efficiency
- Calculate current with real-time feedback
Authoritative online tools:
- Schneider Electric’s PowerCalc: https://www.se.com/ww/en/work/support/resources-and-tools/powercalc/
- Siemens Power Calculators: https://new.siemens.com/global/en/products/automation/topic-areas/industrial-controls/power-calculator.html
Final Notes on Measurement and Instrumentation
- Use true RMS meters to accurately measure current in non-linear or distorted waveforms.
- Clamp meters simplify current measurement without circuit disconnection.
- When measuring or calculating currents for billing or safety, always include a margin (e.g., 125%) to comply with electrical codes such as NEC.