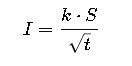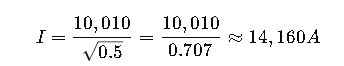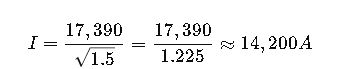Conductor Short-Circuit Capacity Calculator – IEC

The short-circuit withstand capacity of conductors is vital in electrical engineering, ensuring safety, reliability, and compliance. IEC 60949 and IEC 60364-5-54 define methods to calculate adiabatic capacity, verifying conductors withstand stresses.

Conductor Short-Circuit Capacity Calculator — IEC (adiabatic)

Estimate thermally permissible short-circuit current using the adiabatic equation. Enter conductor area (S), fault duration (t) and choose material/insulation (or enter custom k).

Which formula is used?
Adiabatic: I = k × S / √t (equivalently I²·t ≤ k²·S²). k depends on conductor material, insulation, and temperatures.
Where do the k values come from?
Default k values are commonly published in IEC guidance and manufacturer literature (examples: Cu-PVC ≈115, Cu-XLPE ≈143, Al-PVC ≈76). Use actual table values from IEC 60949 / cable manufacturer when available.
When should I not use the adiabatic equation?
If non-adiabatic heating, screen/armour melting, or complex installation conditions apply, use detailed IEC 60949 methods or manufacturer tables.

Core Formula for Short-Circuit Capacity (IEC)

The main formula from IEC 60949 (and referenced in IEC 60364) is the adiabatic equation:

Where:

  • I = permissible short-circuit current (A)
  • k = material constant depending on conductor material and insulation (A·√s / mm²)
  • S = cross-sectional area of the conductor (mm²)
  • t = duration of short-circuit (s)

Detailed Explanation of Variables

  1. Conductor Cross-Section (S, in mm²):
    • Determines thermal mass and ability to withstand heat.
    • Common sizes: 1.5, 2.5, 4, 6, 10, 16, 25, 35, 50, 70, 95, 120, 150, 185, 240, 300, 400, 500, 630 mm².
  2. Time (t, in seconds):
    • Represents fault clearing time.
    • Typical ranges:
      • LV breakers/fuses: 0.1 – 1 s
      • MV/HV relays: 0.2 – 3 s
      • Emergency/back-up scenarios: up to 5 s
  3. Material Constant (k):
    • Derived from material resistivity, specific heat, and permissible final temperature.
    • Common k-values (IEC 60364-5-54):
Material & Insulation TypeInitial Temp (°C)Final Temp (°C)k (A·√s/mm²)
Copper, PVC70160115
Copper, XLPE90250143
Aluminium, PVC7016076
Aluminium, XLPE9025094
Bare copper (earth)30250226

Reference: IEC 60364-5-54

Extended Data Table: Conductor Short-Circuit Capacity (1s Fault Duration)

The following table provides allowable short-circuit current (I) for common conductor sizes, for 1s fault duration, calculated using IEC k-values.

Cross-Section (mm²)Copper PVC (k=115)Copper XLPE (k=143)Aluminium PVC (k=76)Aluminium XLPE (k=94)
1.5173 A220 A114 A141 A
2.5288 A358 A190 A235 A
4460 A572 A304 A376 A
6690 A858 A456 A576 A
101150 A1430 A760 A940 A
161840 A2290 A1216 A1504 A
252875 A3575 A1900 A2350 A
354025 A5005 A2660 A3290 A
505750 A7150 A3800 A4700 A
708050 A10,010 A5320 A6580 A
9510,925 A13,585 A7220 A8930 A
12013,800 A17,160 A9120 A11,280 A
15017,250 A21,450 A11,400 A14,100 A
18521,275 A26,455 A14,060 A17,390 A
24027,600 A34,320 A18,240 A22,560 A
30034,500 A42,900 A22,800 A28,200 A
40046,000 A57,200 A30,400 A37,600 A
50057,500 A71,500 A38,000 A47,000 A
63072,450 A90,090 A47,880 A59,220 A

Step-by-Step Real-World Examples

Case Study 1: LV Distribution Cable (Copper XLPE)

Scenario:

  • 3-phase, 400V LV distribution board.
  • Conductor: Copper XLPE, 70 mm².
  • Fault clearing time: 0.5 s.

Solution:

1.From table: 70 mm², Copper XLPE = 10,010 A (for 1s).

2.For 0.5s:

    3.The cable withstands 14.16 kA for 0.5s.

    4.If the expected short-circuit level at the board is 12 kA, conductor sizing is adequate.

      Case Study 2: MV Aluminium Conductor (XLPE)

      Scenario:

      • 11kV feeder, expected short-circuit level 8 kA.
      • Protection relay trips within 1.5s.
      • Conductor: Aluminium XLPE, 185 mm².

      Solution:

      1.From table: 185 mm² Aluminium XLPE = 17,390 A (for 1s).

      2.For 1.5s:

        3.Allowable withstand = 14.2 kA for 1.5s.

        4.Since required withstand is 8 kA, conductor is more than sufficient.

          Engineering Considerations Beyond the Adiabatic Equation

          1. Non-Adiabatic Conditions:
            • For fault durations < 0.1 s, mechanical forces may dominate instead of thermal effects.
          2. Parallel Conductors:
            • Each conductor must be evaluated independently.
            • Unequal current distribution may reduce actual withstand.
          3. Earthing Conductors:
            • Earth conductors often use bare copper, with higher k-values.
          4. Derating Factors:
            • High ambient temperature.
            • Grouping of cables.
            • Soil resistivity in buried installations.
          5. Verification Against Protection Devices:

          Extended Tables for Multiple Fault Durations

          Because fault clearing times vary widely depending on system voltage, protection scheme, and breaker technology, engineers must verify conductors under different durations. Below are ready-to-use tables derived from IEC k-values.

          Copper XLPE Insulated Conductors (k = 143)

          Cross-Section (mm²)0.2s0.5s1s3s5s
          165124 A3220 A2290 A1323 A1024 A
          3511,122 A6992 A5005 A2890 A2237 A
          7022,223 A13,991 A10,010 A5779 A4470 A
          12038,134 A24,007 A17,160 A9910 A7667 A
          18558,818 A37,000 A26,455 A15,262 A11,818 A
          30095,050 A59,985 A42,900 A24,767 A19,028 A
          500158,300 A99,850 A71,500 A41,300 A31,900 A

          Aluminium XLPE Insulated Conductors (k = 94)

          Cross-Section (mm²)0.2s0.5s1s3s5s
          256160 A3876 A2740 A1582 A1225 A
          5012,320 A7752 A5480 A3164 A2450 A
          9523,400 A14,730 A10,430 A6020 A4660 A
          15037,000 A23,300 A16,520 A9540 A7370 A
          24059,200 A37,250 A26,400 A15,250 A11,800 A
          40098,700 A62,150 A44,000 A25,400 A19,600 A
          630155,400 A97,900 A69,300 A40,000 A30,900 A

          These values are practical look-up references for protection coordination and quick engineering checks.

          Practical Engineering Applications

          Industrial Low-Voltage Switchgear

          • Challenge: In LV systems, fault levels can reach 30–50 kA at the busbars.
          • Role of calculator: Ensures that outgoing feeder cables and busbars can thermally survive faults until breakers clear them.
          • Typical case: 240 mm² copper XLPE cables feeding MCCs withstand up to ~34 kA for 1s, sufficient for modern LV switchgear fault ratings.

          Medium-Voltage Distribution Networks

          • Challenge: Fault levels are usually between 5–25 kA, but protection times are longer (1–3s).
          • Role of calculator: Conductors must be checked not only for magnitude but also duration.
          • Typical case: An 11kV feeder with aluminium 185 mm² XLPE can withstand ~14 kA for 1.5s, covering most distribution networks.

          Earthing and Grounding Conductors

          • Challenge: Earthing conductors must dissipate energy safely during earth faults without damage.
          • Special case: Bare copper conductors with k = 226 have very high withstand capacity.
          • Example: A 70 mm² bare copper earthing conductor can handle over 18 kA for 1s.

          Renewable Energy Systems (Solar & Wind Farms)

          • Challenge: Short-circuit contribution from inverters is typically lower, but clearing times are longer.
          • Example: PV farms may use aluminium conductors with higher lengths, requiring careful IEC calculation to avoid overheating during prolonged faults.

          Common Mistakes in Short-Circuit Capacity Evaluation

          1. Ignoring protection clearing time:
            • Engineers often check only for 1s, but many relays clear in 0.2–0.5s, meaning cables can safely handle higher currents.
          2. Overestimating parallel conductor capacity:
            • Current sharing may not be equal, especially in asymmetric layouts.
          3. Forgetting earthing conductors:
            • Earth faults may last longer, stressing earth conductors more than phase conductors.
          4. Not matching with protective device curves:
            • Conductors must always be verified against I²t clearing energy of the breaker or fuse.

          Related Content