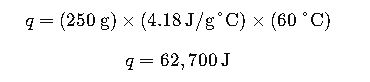Understanding heat transfer calculations is essential across thermodynamics, engineering, environmental science, and culinary science applications. The equation ![]() quantifies heat energy absorbed or released during temperature changes.
quantifies heat energy absorbed or released during temperature changes.
Heat Transfer Calculator (q = mcΔT)
What is q = mcΔT?
Which units should I use?
Formula used
Common Specific Heat Capacities
Specific heat capacity (ccc) is a material-specific property that indicates the amount of heat required to raise the temperature of a unit mass of a substance by one degree Celsius (or Kelvin). Below is a table listing the specific heat capacities of various substances:
| Substance | Specific Heat Capacity (J/g°C) |
|---|---|
| Water (liquid) | 4.18 |
| Ice (solid) | 2.09 |
| Aluminum | 0.90 |
| Copper | 0.39 |
| Iron | 0.45 |
| Lead | 0.13 |
| Gold | 0.13 |
| Silver | 0.24 |
| Air (dry, 0°C) | 1.00 |
| Nitrogen (gas) | 1.04 |
| Oxygen (gas) | 0.92 |
| Hydrogen (gas) | 14.30 |
| Ethanol | 2.44 |
| Mercury (liquid) | 0.14 |
| Concrete | 0.84 |
| Granite | 0.79 |
| Sand | 0.80 |
| Wood | 1.70 |
| Rubber | 1.70 |
| Nylon | 1.70 |
| Wax | 2.20 |
| Asphalt Concrete | 0.90 |
| Coal | 1.38 |
| Glass | 0.84 |
| Quartz | 0.74 |
| Kevlar | 1.42 |
| Polyamide-Nylon | 1.50 |
| Beryllium Copper | 0.38 |
| Tungsten | 0.13 |
| Uranium | 0.12 |
Note: Values are approximate and can vary based on temperature and phase.
Detailed Breakdown of the Heat Transfer Equation
The equation ![]() is derived from the first law of thermodynamics, which states that energy cannot be created or destroyed, only transferred or converted. Here’s a detailed explanation of each variable:
is derived from the first law of thermodynamics, which states that energy cannot be created or destroyed, only transferred or converted. Here’s a detailed explanation of each variable:
- q (Heat Energy, J): Represents the amount of thermal energy absorbed or released by the substance. It is measured in joules (J) in the SI system.
- m (Mass, g or kg): The mass of the substance involved in the heat transfer. It is typically measured in grams (g) or kilograms (kg).
- c (Specific Heat Capacity, J/g°C or J/kg°C): A material-specific constant that indicates how much heat is required to raise the temperature of a unit mass of the substance by one degree Celsius (or Kelvin).
- ΔT (Temperature Change, °C or K): The difference between the final and initial temperatures of the substance. It is calculated as
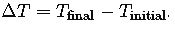
Units Consistency
For accurate calculations, it’s crucial to ensure that the units are consistent:
- If mass is in grams, specific heat capacity should be in J/g°C.
- If mass is in kilograms, specific heat capacity should be in J/kg°C.
Real-World Examples of Heat Transfer Calculations
Example 1: Heating Water in a Laboratory
Problem: Calculate the amount of heat required to raise the temperature of 250 g of water from 20°C to 80°C.
Given:
- Mass of water (m) = 250 g
- Specific heat capacity of water (ccc) = 4.18 J/g°C
- Temperature change (ΔT) = 80°C – 20°C = 60°C
Solution:
Using the equation q=mcΔT
Therefore, 62.7 kJ of heat is required.
Example 2: Cooling of a Metal Block
Problem: A 500 g block of copper is heated from 25°C to 75°C. Calculate the heat absorbed by the copper.
Given:
- Mass of copper (m) = 500 g
- Specific heat capacity of copper (ccc) = 0.39 J/g°C
- Temperature change (ΔT) = 75°C – 25°C = 50°C
Solution:
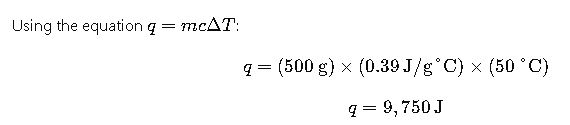
Thus, 9.75 kJ of heat is absorbed by the copper block.
Applications and Importance in Engineering and Science
The calculation of heat transfer is essential in various fields:
- Engineering: Designing heating and cooling systems, such as radiators, heat exchangers, and air conditioning units, requires precise calculations of heat transfer to ensure efficiency and safety.
- Environmental Science: Understanding heat transfer helps in modeling climate change, studying ocean currents, and assessing the impact of human activities on global temperatures.
- Culinary Arts: Chefs and food scientists use heat transfer calculations to optimize cooking processes, ensuring food safety and quality.
- Material Science: Engineers assess the thermal properties of materials to select appropriate substances for specific applications, such as insulation materials or heat-resistant components.
Advanced Considerations and Complexities
While the equation ![]() is widely applicable, several factors can influence heat transfer:
is widely applicable, several factors can influence heat transfer:
- Phase Changes: During phase transitions (e.g., melting, boiling), the heat energy goes into changing the state of the substance rather than increasing its temperature. The heat involved in these processes is calculated using latent heat equations.
- Temperature Dependence of Specific Heat: The specific heat capacity of a substance can vary with temperature. For precise calculations, this variation must be considered.
- Non-Uniform Heating: In real-world scenarios, heat may not be uniformly distributed, leading to temperature gradients within the substance. Advanced models, such as Fourier’s law of heat conduction, are used to analyze such situations.
Conclusion
The equation ![]() serves as a fundamental tool in understanding and calculating heat transfer. Its applications span various disciplines, highlighting its importance in both theoretical studies and practical applications. By considering factors such as phase changes, temperature dependence of specific heat, and non-uniform heating, more accurate and complex models can be developed to analyze heat transfer in diverse scenarios.
serves as a fundamental tool in understanding and calculating heat transfer. Its applications span various disciplines, highlighting its importance in both theoretical studies and practical applications. By considering factors such as phase changes, temperature dependence of specific heat, and non-uniform heating, more accurate and complex models can be developed to analyze heat transfer in diverse scenarios.
For further reading and more detailed information on specific heat capacities and heat transfer calculations, consider exploring the following resources:
- Wikipedia: Specific Heat Capacity
- Engineering Toolbox: Specific Heat of Materials
- LibreTexts: Energy and Heat Capacity Calculations
By delving into these resources, readers can gain a deeper understanding of the principles governing heat transfer and their applications in various fields.