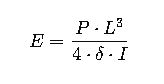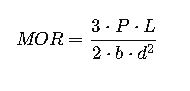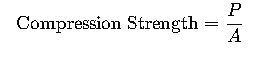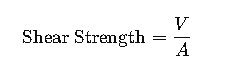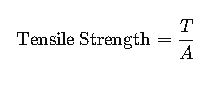Wood, as an engineering material, presents unique challenges and opportunities due to its orthotropic characteristics. Understanding mechanical properties, calculation methods, and behavior is crucial for accurate structural design. This guide explains wood calculation in detail, providing formulas, tables, and examples for practical applications.
Watts ↔ Amperes Calculator
Mechanical Properties of Wood
Wood’s mechanical properties vary significantly across species and are influenced by factors such as moisture content, grain orientation, and density. The primary mechanical properties include:
- Modulus of Elasticity (MOE): Measures stiffness; varies with species and grain orientation.
- Modulus of Rupture (MOR): Indicates the maximum bending stress before failure.
- Compression Strength Parallel to Grain: Maximum compressive stress along the grain.
- Shear Strength Parallel to Grain: Resistance to sliding forces along the grain.
- Tensile Strength Perpendicular to Grain: Resistance to pulling forces across the grain.
- Hardness: Resistance to indentation and wear.
Wood Properties Table
| Species | MOE (MPa) | MOR (MPa) | Compression (MPa) | Shear (MPa) | Tensile (MPa) | Hardness (N) |
|---|---|---|---|---|---|---|
| Oak (Quercus spp.) | 12,000 | 90 | 50 | 10 | 10 | 500 |
| Pine (Pinus spp.) | 9,000 | 70 | 40 | 8 | 8 | 400 |
| Maple (Acer spp.) | 11,000 | 85 | 45 | 9 | 9 | 450 |
| Cherry (Prunus spp.) | 10,500 | 80 | 42 | 8.5 | 8.5 | 460 |
| Walnut (Juglans spp.) | 13,000 | 95 | 55 | 11 | 11 | 520 |
Note: Values are approximate and can vary based on specific conditions and treatments.
Formulas for Wood Calculation
1. Modulus of Elasticity (MOE)
The Modulus of Elasticity is calculated using the formula:
Where:
- E= Modulus of Elasticity (MPa)
- P= Applied load (N)
- L= Length of the beam (m)
- δ= Deflection at the center (m)
- I= Moment of inertia of the cross-section (m⁴)
2. Modulus of Rupture (MOR)
The Modulus of Rupture is determined from bending tests:
Where:
- P= Maximum load at failure (N)
- L= Span length (m)
- b= Width of the specimen (m)
- d= Depth of the specimen (m)
3. Compression Strength Parallel to Grain
Calculated using:
Where:
- P= Applied compressive load (N)
- A= Cross-sectional area (m²)
4. Shear Strength Parallel to Grain
Determined by:
Where:
- V= Shear force (N)
- A= Cross-sectional area (m²)
5. Tensile Strength Perpendicular to Grain
Calculated using:
Where:
- T= Tensile force (N)
- A= Cross-sectional area (m²)
Real-World Examples
Example 1: Beam Design for a Residential Floor
Problem: Design a wooden beam to support a floor load of 5 kN/m² over a span of 4 meters. The beam is made of oak with a width of 0.1 m and a depth of 0.3 m.

Conclusion: The deflection is within acceptable limits for residential floors.
Example 2: Column Compression Analysis
Problem: Analyze a vertical oak column with a height of 3 meters and a cross-sectional area of 0.02 m² under a compressive load of 50 kN.
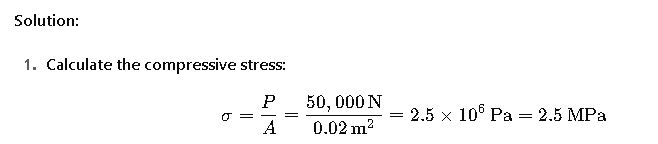
Conclusion: The compressive stress is well below the typical compressive strength of oak, indicating the column is safe under the given load.
Advanced Considerations
Moisture Content Effects
Wood’s mechanical properties are highly sensitive to moisture content. An increase in moisture content typically decreases strength properties and increases the risk of decay.
Temperature Effects
High temperatures can reduce wood’s strength and stiffness, while low temperatures may make it more brittle.
Grain Orientation
The direction of the grain affects the material’s strength. Wood is strongest along the grain and weakest perpendicular to it.
References
- Forest Products Laboratory. (2010). Wood Handbook: Wood as an Engineering Material. General Technical Report FPL–GTR–190.
- Rammer, D. R. (2005). Structural Analysis Equations. Forest Products Laboratory.
- Workshop Companion. (n.d.). Mechanical Properties of Wood.
- Engineering ToolBox. (n.d.). Young’s Modulus of Elasticity – Values for Common Materials.