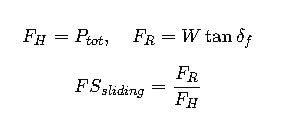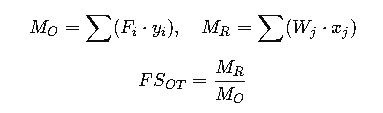Comprehensive technical guide for engineers on retaining wall calculations, covering formulas, tables, and variables, explanations. Includes sliding, overturning, bearing-capacity checks, Mononobe-Okabe seismic method, and two detailed worked examples with solutions.
Retaining Wall Quick-Check Calculator
Estimate active earth pressure, overturning & sliding safety factors, and simple bearing check. Use units: meters (m), kN/m³, kN/m².
What assumptions does this calculator use?
• Simple rectangular cross-section: wall stem (constant thickness) + rectangular base slab.
• Unit length = 1 m (per meter run). Concrete weight and soil units in kN/m³ and kN/m².
• This is a quick-check only — hire a licensed engineer for final design.
Formulas used (brief)
Triangular earth thrust: P_tri = 0.5·γ·H²·Ka.
Surcharge thrust: P_q = q·H·Ka.
Total lateral force: P = P_tri + P_q (kN per meter).
Overturning moment about toe: M_o = P_tri·(H/3) + P_q·(H/2).
Weight (per meter): W = γc·(t_s·H + B·t_b) (kN/m). Resisting moment approx: M_r = W·(B/2).
FS_overturning = M_r / M_o. FS_sliding = (W·μ) / P. Bearing pressure check uses resultant eccentricity and rectangular footing formula.
Why use μ = tan(2φ/3) if blank?
Limitations
1. Extensive tables of common values (engineer’s quick tables)
These tables are per-meter length (1 m) unless stated otherwise. Values are typical ranges used in preliminary design; site investigation (laboratory tests / CPT / SPT) must be used for final design.
Table A — Typical unit weights, friction angles and cohesion (common soils)
| Soil type | Typical unit weight γ (kN/m³) | Typical unit weight (lb/ft³) | Typical φ′ (deg) | Typical cohesion c′ (kPa) |
|---|---|---|---|---|
| Clean dry sand / gravel | 18 – 20 | 115 – 125 | 30 – 40 | ~0 (drained) |
| Loose sand | 16 – 18 | 100 – 115 | 25 – 30 | ~0 |
| Dense sand | 18 – 20 | 115 – 125 | 35 – 45 | ~0 |
| Silty sand / silt (partly cohesive) | 17 – 19 | 105 – 120 | 20 – 30 | 0 – 10 |
| Clay (normally consolidated) | 17 – 19 | 105 – 120 | 10 – 25 | 10 – 50 |
| Firm clay (stiffer) | 18 – 20 | 115 – 125 | 15 – 30 | 20 – 150 |
| Gravelly fill | 19 – 21 | 120 – 130 | 30 – 40 | ~0 – small |
| Rock (intact) | 25 – 27 | 160 – 170 | n/a | very large |
Table B — Rankine earth-pressure coefficients (Ka, Kp) for common φ (degrees)
| φ (deg) | Ka (active) | Kp (passive) |
|---|---|---|
| 0 | 1.0000 | 1.0000 |
| 5 | 0.8397 | 1.1910 |
| 10 | 0.7041 | 1.4203 |
| 15 | 0.5888 | 1.6984 |
| 20 | 0.4903 | 2.0396 |
| 25 | 0.4059 | 2.4639 |
| 30 | 0.3333 | 3.0000 |
| 35 | 0.2710 | 3.6902 |
| 40 | 0.2174 | 4.5989 |
| 45 | 0.1716 | 5.8284 |
Table C — Typical design safety factors (common practice)
| Limit state | Typical recommended minimum factor |
|---|---|
| Sliding (static) | FS ≥ 1.50 |
| Overturning (moment) | FS ≥ 1.50 – 2.00 |
| Bearing capacity | FS ≈ 2.5 – 3.0 |
| Seismic pseudo-static cases | FS ≥ 1.1 (sliding under earthquake) |
2. Complete list of formulas for retaining-wall calculations and variable definitions
2.1 Lateral earth pressure (Rankine — cohesionless, horizontal backfill)
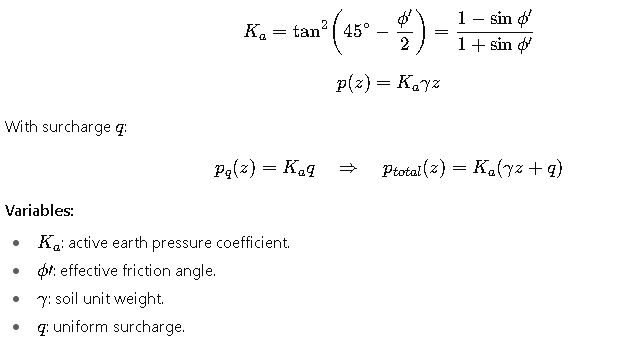
2.2 Coulomb earth pressure (includes wall friction δ and backfill slope β)
General form considers:
- ϕ= soil friction angle
- δ= wall-soil friction angle (0 ≤ δ ≤ φ)
- β= backfill surface slope
- θ= wall face inclination
Practical δ: between 1/3 φ and 2/3 φ.
2.3 Cohesive soils (Rankine extension)
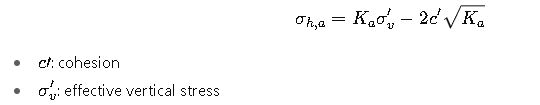
2.4 Hydrostatic (pore-water) pressure
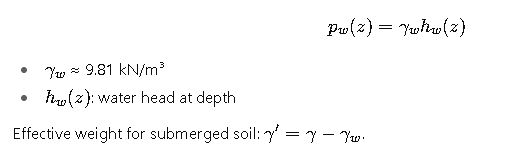
2.5 Seismic earth pressure — Mononobe-Okabe (pseudo-static)
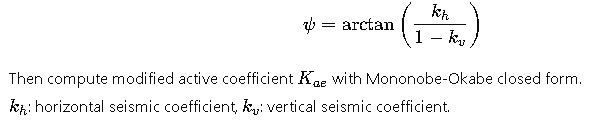
2.6 Resultant force and line of action
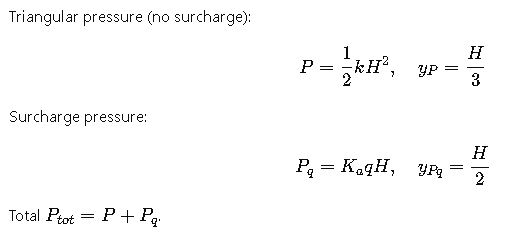
2.7 Sliding check
2.8 Overturning check
2.9 Bearing capacity (Terzaghi simplified)
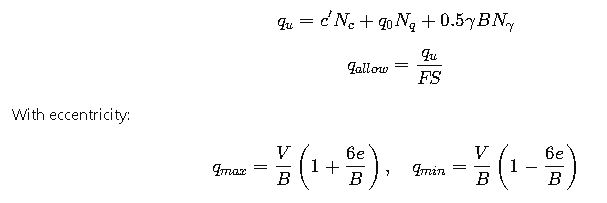
3. Two detailed real-world worked examples
Example 1 — Small garden gravity wall
- H = 1.5 m
- φ′ = 30°, Ka = 0.3333
- γ = 18 kN/m³
- Concrete γc = 24 kN/m³
- Wall thickness = 0.5 m, W = 18.0 kN/m
- δ = 20°
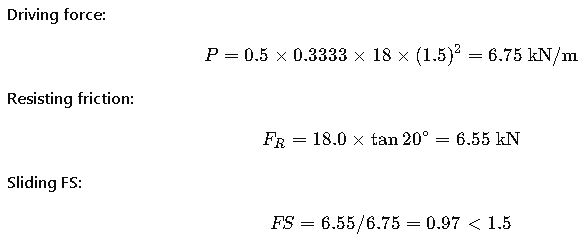
Result: Not safe. Increase base width, add key, or change wall type.
Result: Fails all checks → requires wider base, thicker sections, or alternative design.
4. Practical design notes
- Always begin with site investigation: φ′, c′, γ, groundwater.
- Drainage is critical: design for full water pressure unless proven otherwise.
- Interface friction δ: assume 1/3 φ to 2/3 φ depending on roughness.
- Passive resistance is unreliable; use only if proven.
- Seismic design: use Mononobe-Okabe or advanced analysis.
- Bearing capacity: check eccentricity and ensure qmax ≤ qallow.
- Surcharges: always include traffic, compaction, or storage loads.
- Run sensitivity checks varying φ, water depth, load assumptions.
5. Checklist for calculation workflow
- Collect soil parameters.
- Select wall type.
- Compute earth pressures.
- Add surcharge, water, seismic.
- Compute resultant forces.
- Compute wall weight and centroid.
- Check sliding FS ≥ 1.5.
- Check overturning FS ≥ 1.5–2.0.
- Check bearing capacity FS ≥ 2.5–3.0.
- Iterate geometry or reinforce as required.
6. Engineering tips
- Preliminary base width for cantilever walls: about 0.5–0.6H.
- Use Coulomb if wall friction or sloping backfill exists.
- Model worst-case groundwater if uncertain.
- Tall or critical walls: use advanced numerical modeling.