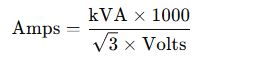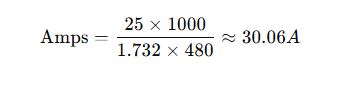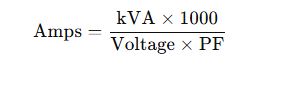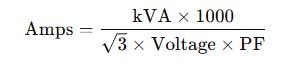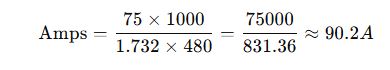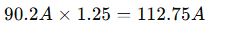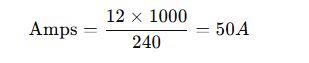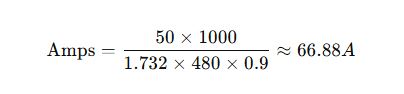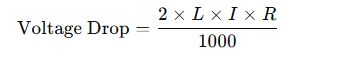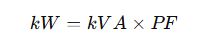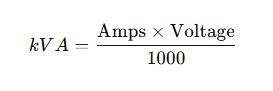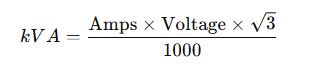Convert kVA to Amps instantly: enter kVA, choose phase and voltage; get precise amperage results.
Use I=(kVA×1000)/(√3×V) three-phase or I=(kVA×1000)/V single-phase; accurate outputs for any voltage, includes copy, share, reset.
kVA to Amps (A) Calculator
How to convert kVA to Amps in three-phase?
What about single-phase or two-phase?
kVA vs kW — what’s the difference?
Why does my current differ from the nameplate?
kVA to Amps Conversion Chart (Single Phase and Three Phase)
Table 1: kVA to Amps (Single Phase) – Common Voltages
| kVA | Voltage (V) | Amps (A) |
|---|---|---|
| 1 | 120 | 8.33 |
| 1 | 240 | 4.17 |
| 2 | 240 | 8.33 |
| 3 | 208 | 14.42 |
| 5 | 240 | 20.83 |
| 10 | 240 | 41.67 |
| 15 | 240 | 62.5 |
| 20 | 480 | 41.67 |
| 25 | 480 | 52.08 |
| 30 | 600 | 50 |
| 50 | 240 | 208.33 |
| 75 | 480 | 156.25 |
| 100 | 600 | 166.67 |
Table 2: kVA to Amps (Three Phase, Line-to-Line)
| kVA | Voltage (V) | Amps (A) |
|---|---|---|
| 1 | 208 | 2.78 |
| 2 | 208 | 5.55 |
| 5 | 208 | 13.87 |
| 10 | 208 | 27.74 |
| 15 | 240 | 36.1 |
| 20 | 480 | 24.05 |
| 25 | 480 | 30.06 |
| 30 | 600 | 28.87 |
| 50 | 480 | 60.12 |
| 75 | 480 | 90.18 |
| 100 | 600 | 96.23 |
| 150 | 480 | 180.37 |
| 200 | 600 | 192.45 |
Note: These values assume a power factor (PF) of 1.0 for simplicity. For real applications, PF corrections are necessary.
kVA to Amps Formulas and Detailed Explanation
Formula for Single Phase
Where:
- kVA: Kilovolt-Amperes (Apparent Power)
- 1000: Conversion factor from kVA to VA
- Volts: Voltage in volts (V)
- Amps: Output current in amperes (A)
Example with values:
- kVA = 10
- Voltage = 240V
Formula for Three Phase
Where:
- √3 ≈ 1.732 (Three-phase power factor constant)
- The rest of the variables are as defined above.
Example with values:
- kVA = 25
- Voltage = 480V
Optional: Incorporating Power Factor (PF)
When power factor is involved (real-world applications), the formulas become:
- Single-phase:
- Three-phase:
Typical Power Factors:
- Resistive Load (Heaters, Incandescent Lamps): PF = 1.0
- Motors (Inductive Loads): PF = 0.8 to 0.9
- UPS Systems: PF = 0.7 to 0.95
Real-World Applications and Use Cases
Case Study 1: Sizing a Transformer for an Industrial Facility
Scenario:
An industrial facility needs to power several 3-phase motors using a transformer. The total load is 75 kVA at 480V.
Step 1: Use 3-phase formula
Step 2: Select a transformer
- A transformer rated 75 kVA with a 480V secondary output can handle approx. 90A.
- Ensure cables and breakers are rated for at least 125% of load →
Outcome:
Engineer selects a 75 kVA, 480V transformer with 125A-rated protection.
Case Study 2: Designing a Residential Backup Generator
Scenario:
A home requires a single-phase backup generator to handle 12 kVA at 240V.
Step 1: Use single-phase formula
Step 2: Check compatibility with panel and wiring
- 50A output = suitable for a 60A breaker
- Wire size recommendation: 6 AWG copper
Outcome:
Homeowner installs a 12 kVA, 240V generator with a 60A panel interface and appropriate transfer switch.
How to Use Online kVA to Amp Calculators Efficiently
While manual formulas are essential for understanding, online calculators significantly speed up the process and reduce errors. Here’s a step-by-step on how to use them correctly:
Inputs Typically Required:
- Power in kVA
- Voltage (V)
- Phase Type – Single or Three Phase
- Power Factor (optional)
Example Using an Online Calculator:
- Input: 50 kVA, 480 V, 3-phase, PF = 0.9
- Output:
Transformer Integration: kVA to Amp in Transformer Sizing
Correctly converting kVA to amps ensures transformer primary and secondary windings are not overloaded, prolonging lifespan and ensuring safety.
Step-by-Step Guide:
- Identify Load Requirements (in kVA)
- Convert to Amps using formulas above
- Add Safety Factor (typically 1.25x or more)
- Choose Transformer Size matching or slightly exceeding peak load
Example:
For a 3-phase load of 100 kVA at 480V
→ Design for: 150A system minimum
→ Select: 112.5 kVA transformer or next size up (per IEEE Std C57.12.00)
Expert Insights: Advanced kVA to Amp Considerations
Derating for Temperature and Altitude
Transformer capacity drops with higher temperatures and altitudes. Apply derating factors per IEEE C57.91.
- Example: At 1000 meters altitude and 40°C, a 100 kVA transformer may be derated to 85 kVA.
Voltage Drop Considerations
For long runs, current increases due to voltage drop. Use voltage drop calculators or formulas:
Where:
- L = Length of run (m)
- I = Current in amps
- R = Resistance (Ω/km)
Frequently Asked Questions (FAQs)
1. Can I convert kVA to amps without knowing voltage?
No. Voltage is essential for conversion. kVA is apparent power, while amps depend on potential difference.
2. What is the difference between kVA and kW?
- kVA = Apparent power (includes reactive + real power)
- kW = Real power (useful power)
3. How do I convert amps to kVA?
Use the reverse formula:
- Single phase:
- Three phase:
Recommended Resources and External Links
- IEEE Power Standards
- NEC – National Electrical Code
- RapidTables – kVA to Amps Calculator
- EngineeringToolBox
- ABB Transformer Selection Guide