Below are authoritative, ISA-based lookup tables for common barometric pressures, showing hPa and inHg values. Corresponding altitudes in meters and feet are derived under standard ISA assumptions for reference.
Barometric Pressure → Altitude Converter
Convert pressure (hPa / inHg) to altitude. Choose ISA (barometric) or Hypsometric (use temperature) method. Results in meters and feet.
Which method should I use?
Units
Formulas used
h = (T₀ / L) · (1 − (P / P₀)^(R·L / g))
where T₀ = 288.15 K, L = 0.0065 K/m, R = 287.053 J/(kg·K), g = 9.80665 m/s².
Hypsometric formula:
h = (R · T_mean / g) · ln(P₀ / P) — requires mean temperature in K.
Quick Reference Tables — Barometric Pressure → Altitude (ISA-based)
Below are authoritative, ISA-based lookup tables for common barometric pressures. Values show pressure in hPa (mbar), equivalent inches of mercury (inHg), and corresponding altitude in meters and feet. These are geometric altitudes derived under the International Standard Atmosphere (ISA) assumptions (tropospheric lapse rate up to 11 km, then first isothermal layer). Values are for quick technical reference and assume standard sea-level pressure (1013.25 hPa) and standard temperature profile.
Notes: these altitudes assume ISA. They are pressure-derived altitudes and do not include local temperature or humidity corrections. For operational accuracy (aviation, surveying, meteorology) apply QNH/QFE, temperature/virtual-temperature corrections, and any geopotential adjustments.
| Pressure (hPa) | Pressure (inHg) | Altitude (m) | Altitude (ft) |
|---|---|---|---|
| 1080 | 31.8924 | -541.38 | -1,776.20 |
| 1065 | 31.3844 | -425.14 | -1,394.50 |
| 1050 | 31.0065 | -301.52 | -989.23 |
| 1035 | 30.5380 | -171.22 | -561.62 |
| 1025 | 30.2682 | -97.35 | -319.40 |
| 1013.25 (MSL std) | 29.9213 | 0.00 | 0.00 |
| 1000 | 29.5300 | 110.88 | 363.79 |
| 990 | 29.2358 | 196.90 | 645.64 |
| 980 | 28.9394 | 280.53 | 920.38 |
| 965 | 28.4398 | 393.08 | 1,289.04 |
| 950 | 28.0535 | 540.34 | 1,772.76 |
| 940 | 27.7593 | 647.99 | 2,125.33 |
| 925 | 27.3152 | 761.97 | 2,499.89 |
| 910 | 26.8735 | 876.87 | 2,876.18 |
| 900 | 26.5770 | 988.50 | 3,243.11 |
| 880 | 25.9864 | 1,213.94 | 3,984.16 |
| 850 | 25.1005 | 1,457.30 | 4,781.17 |
| 825 | 24.3814 | 1,658.88 | 5,441.24 |
| 800 | 23.6240 | 1,948.99 | 6,394.32 |
| 775 | 22.8667 | 2,139.28 | 7,018.01 |
| 750 | 22.1475 | 2,466.22 | 8,091.29 |
| 725 | 21.4292 | 2,751.07 | 9,028.22 |
| 700 | 20.6710 | 3,012.18 | 9,882.48 |
| 675 | 19.9137 | 3,321.12 | 10,892.72 |
| 650 | 19.1945 | 3,590.69 | 11,780.46 |
| 625 | 18.4753 | 3,905.05 | 12,815.31 |
| 600 | 17.7180 | 4,206.42 | 13,800.60 |
| 575 | 16.9607 | 4,560.77 | 14,968.34 |
| 550 | 16.2415 | 4,865.21 | 15,961.99 |
| 525 | 15.5223 | 5,226.52 | 17,138.51 |
| 500 | 14.7650 | 5,574.43 | 18,288.82 |
| 475 | 14.0078 | 5,964.11 | 19,573.77 |
| 450 | 13.2885 | 6,343.62 | 20,812.39 |
| 425 | 12.5693 | 6,774.05 | 22,238.29 |
| 400 | 11.8120 | 7,185.43 | 23,574.25 |
| 375 | 11.0548 | 7,652.82 | 25,089.86 |
| 350 | 10.3355 | 8,117.26 | 26,631.44 |
| 325 | 9.6162 | 8,627.80 | 28,303.41 |
| 300 | 8.8590 | 9,163.95 | 30,065.46 |
| 275 | 8.1018 | 9,742.88 | 31,968.99 |
| 250 | 7.3825 | 10,362.94 | 33,999.14 |
| 225 | 6.6633 | 11,025.79 | 36,180.36 |
| 200 | 5.9060 | 11,784.04 | 38,661.55 |
| 175 | 5.1488 | 12,615.12 | 41,386.45 |
| 150 | 4.4295 | 13,608.41 | 44,647.02 |
| 125 | 3.7102 | 14,776.89 | 48,492.45 |
| 100 | 2.9530 | 16,179.71 | 53,083.05 |
Physical Principles and Why the Conversion Works
Converting barometric pressure to altitude relies on two fundamental physical relations:
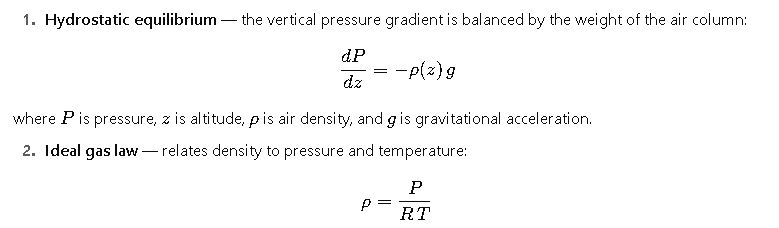
where R is the specific gas constant for dry air and T is absolute temperature.
Combining them and integrating vertically with an assumed temperature profile produces the hypsometric equation and barometric formulas that provide closed-form relationships between pressure and altitude under specified assumptions (e.g., linear lapse rate — the troposphere — or isothermal layers).
Two widely used formula families:
- Hypsometric equation — the general, accurate relation for two pressure surfaces if the mean virtual temperature between them is known.
- Barometric formula with constant lapse rate — closed-form inversion that yields altitude directly when temperature decreases linearly with height (standard troposphere assumption).
Core Formulas, Derivations and Variable Definitions
Below are the canonical equations, with definitions and typical values.
1) Hydrostatic differential equation (starting point)

2) Hypsometric equation (general)
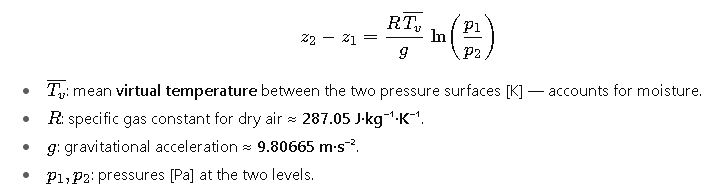
The hypsometric equation is preferred when you have measured temperature (or can compute virtual temperature) because it removes the largest error source: temperature differences from ISA.
3) Barometric formula with linear lapse rate (troposphere)
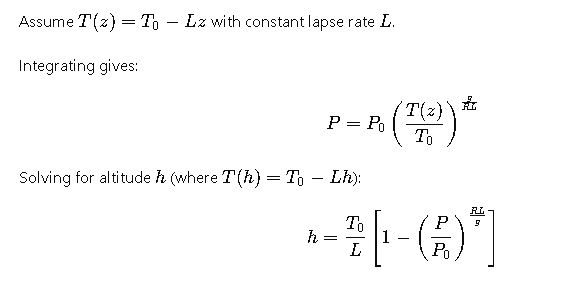
Standard ISA constants:
- P0=101325 PaP_0 = 101325\ \text{Pa}P0=101325 Pa (1013.25 hPa)
- T0=288.15 KT_0 = 288.15\ \text{K}T0=288.15 K (15 °C)
- L=0.0065 K\cdotpm−1L = 0.0065\ \text{K·m}^{-1}L=0.0065 K\cdotpm−1
- R=287.05287 J\cdotpkg−1\cdotpK−1R = 287.05287\ \text{J·kg}^{-1}\text{·K}^{-1}R=287.05287 J\cdotpkg−1\cdotpK−1
- g=9.80665 m\cdotps−2g = 9.80665\ \text{m·s}^{-2}g=9.80665 m\cdotps−2
From these, T0/L≈44330.769 mT_0/L \approx 44330.769\ \text{m}T0/L≈44330.769 m and the exponent (RL)/g≈0.190263(R L)/g \approx 0.190263(RL)/g≈0.190263. That gives the frequently used approximation: h≈44330[1−(PP0)0.190263] (meters)h \approx 44330 \left[1 – \left(\frac{P}{P_0}\right)^{0.190263}\right]\ \text{(meters)}h≈44330[1−(P0P)0.190263] (meters)
4) Isothermal layer formula (L = 0)
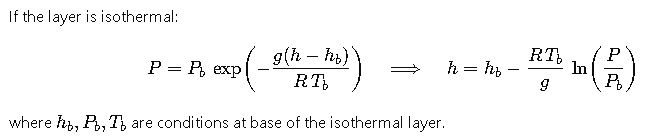
This applies to layers such as the lower stratosphere in standard atmosphere models.
5) Unit conversions (practical)
- 1 hPa (millibar) = 100 Pa
- 1 inHg ≈ 33.8639 hPa
- 1 m = 3.280839895 ft
Typical Variable Values & Practical Meaning

Operationally:
- Use pressure altitude (set altimeter to 1013.25 hPa) when flying above transition level / in standardized aviation procedures.
- Use QNH (local sea-level reduced pressure) to obtain altitude above mean sea level on altimeter.
- For high-precision tasks (surveying), use hypsometric equation with measured mean virtual temperature.
Two Detailed Real-World Case Studies (worked)
All arithmetic shown with sufficient precision; rounds only for display.
Case Study 1 — Quick conversion: handheld barometer reading
Problem: Handheld barometer reads 925.0 hPa. Determine altitude under ISA assumptions (meters and feet).

Result: ISA altitude ≈ 762.0 m (≈ 2,500 ft). This is the same value commonly used in aviation as pressure altitude when QNH is standard.
Case Study 2 — Aviation / meteorology: compute QNH (sea-level reduced pressure) using hypsometric equation

Result: QNH ≈ 996.3 hPa. If a pilot set this QNH, their altimeter would read the correct altitude above mean sea level for that station. This calculation shows how surface pressure, station elevation and mean-layer temperature combine to determine sea-level pressure.
Practical Corrections, Common Error Sources, and Operational Notes
- Temperature deviations from ISA — the dominant error. Warm columns make true altitude higher than ISA-based pressure altitude; cold columns make it lower. Use hypsometric equation with measured mean virtual temperature to correct.
- Humidity (virtual temperature) — moist air is less dense than dry air at same T and P. Use virtual temperature corrections for accurate vertical distances.
- QNH vs. pressure altitude — using standard sea-level pressure (1013.25 hPa) produces pressure altitude; using local QNH yields altitude above mean sea level. Pilots switch between these depending on phase of flight.
- Geopotential vs. geometric altitude — some atmospheric tables use geopotential altitude for convenience; for precise geodesy convert between geopotential and geometric altitude using Earth-radius corrections.
- Local gravity variations — ggg varies with latitude and elevation. For most practical engineering tasks the standard value suffices; for geodesy use local gravity.
- Instrument errors and sensor calibration — membrane, aneroid, mercury and MEMS sensors have different accuracies and calibration protocols. Regular calibration and temperature compensation are necessary for reliable altitude reporting.
- Layered atmosphere — the ISA is piecewise. For pressures corresponding to above-troposphere layers, use correct layer constants and isothermal formulas for inversion.