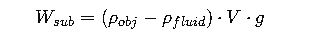Archimedes’ principle underpins fluid mechanics and engineering, describing body–fluid interactions during immersion processes. Accurately determining submerged apparent weight is crucial across naval, offshore, civil, biomedical, and industrial engineering applications.
Submerged Weight Calculator — Archimedes’ Principle
Calculate buoyant force, true weight, and apparent weight for any fully submerged object. Units: SI (kg, m³, N).
What formulas does this use?
Weight of object: W = m · g (or W = ρobject · V · g)
Apparent weight: Wapparent = W − Fb.
How to provide inputs?
Units and assumptions
Core Equations for Submerged Weight
The general equation for the apparent weight Wsub of an object submerged in a fluid is:

1. True Weight in Air
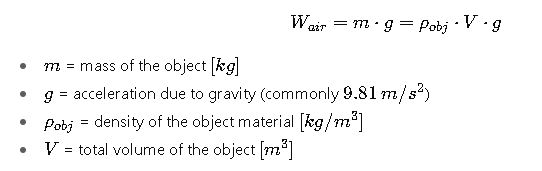
2. Buoyant Force
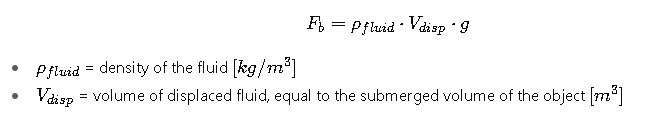

3. Apparent Weight Equation
This compact form is the most practical for engineers, as it highlights the difference in densities as the governing factor.
Variables and Typical Engineering Values
To apply these formulas, engineers frequently rely on standard reference densities for materials and fluids. The following table compiles common values used in submerged weight calculations.
Extended Table of Densities and Submerged Weights
The table below shows true weight, buoyant force, and submerged weight for a 0.01 m³ object made of different materials when fully immersed in fresh water (ρ = 1000 kg/m³). Gravity is assumed as 9.81 m/s².
| Material | Density ρobj\rho_{obj}ρobj (kg/m³) | True Weight in Air (N) | Buoyant Force (N) | Apparent Weight in Water (N) |
|---|---|---|---|---|
| Aluminum | 2700 | 265.0 | 98.1 | 166.9 |
| Brass | 8500 | 834.0 | 98.1 | 735.9 |
| Concrete | 2400 | 235.4 | 98.1 | 137.3 |
| Copper | 8960 | 879.0 | 98.1 | 780.9 |
| Glass | 2500 | 245.3 | 98.1 | 147.2 |
| Granite | 2700 | 265.0 | 98.1 | 166.9 |
| Iron | 7870 | 771.0 | 98.1 | 672.9 |
| Lead | 11340 | 1113.0 | 98.1 | 1014.9 |
| Plastic (PE-HD) | 950 | 93.2 | 98.1 | -4.9 (floats) |
| Steel (mild) | 7850 | 770.0 | 98.1 | 671.9 |
| Titanium | 4500 | 441.5 | 98.1 | 343.4 |
| Wood (Oak) | 700 | 68.7 | 98.1 | -29.4 (floats) |
| Wood (Pine) | 500 | 49.1 | 98.1 | -49.0 (floats strongly) |
Notes:
- Negative submerged weight means the buoyant force exceeds the object’s true weight, and the object floats.
- Engineering applications often require correction factors for salinity, temperature, or pressure, particularly in marine and offshore industries.
Practical Notes on Variables
- Gravity (g): While 9.81 m/s² is standard, local variations due to latitude and elevation can affect precision in sensitive applications.
- Fluid Density (ρfluid):
- Fresh water at 4 °C: ~1000 kg/m³
- Seawater (average salinity): ~1025–1030 kg/m³
- Oil: 800–950 kg/m³
- Mercury: 13,600 kg/m³
- Object Density (ρobj): Can vary with alloy composition, porosity, or manufacturing method. For structural analysis, engineers often use design values from standards such as ASM International.
Reference Tables for Submerged Weights in Different Fluids
The submerged weight of an object depends strongly on the fluid in which it is immersed. While fresh water is the most common case in textbooks, engineers often work with seawater, oils, and other industrial fluids. The following extended table compares the submerged weights of the same 0.01 m³ object for different materials in several fluids.
Table: Submerged Weights in Freshwater, Seawater, Oil, and Mercury
| Material | True Weight (N) | Submerged in Freshwater (N) | Submerged in Seawater (N) | Submerged in Oil (N) | Submerged in Mercury (N) |
|---|---|---|---|---|---|
| Aluminum | 265.0 | 166.9 | 161.4 | 186.8 | -1068.0 (floats strongly) |
| Brass | 834.0 | 735.9 | 730.4 | 755.8 | -499.0 (floats strongly) |
| Concrete | 235.4 | 137.3 | 131.8 | 157.2 | -1096.6 (floats strongly) |
| Iron | 771.0 | 672.9 | 667.4 | 692.8 | -562.0 (floats strongly) |
| Lead | 1113.0 | 1014.9 | 1009.4 | 1034.8 | -220.0 (floats strongly) |
| Steel | 770.0 | 671.9 | 666.4 | 691.8 | -563.0 (floats strongly) |
| Titanium | 441.5 | 343.4 | 337.9 | 363.3 | -891.5 (floats strongly) |
| Oak Wood | 68.7 | -29.4 (floats) | -34.9 (floats) | -9.5 (neutral) | -1196.1 (floats strongly) |
Key engineering observations:
- Seawater, being slightly denser than freshwater, further reduces apparent weight, which is critical in offshore design.
- Light oils, often less dense than water, result in higher apparent weights compared to freshwater.
- Mercury is so dense that almost all common engineering materials float.
Industrial Relevance of Submerged Weight Calculations
Engineers rarely calculate submerged weight for academic purposes alone. These values directly influence:
- Marine and Offshore Engineering: Mooring, anchoring, and subsea pipeline stability require precise determination of effective submerged weight.
- Civil Engineering: Submerged weight affects the stability of foundations, caissons, and retaining structures placed below water tables.
- Mining and Dredging: Equipment and ore handling underwater depend on buoyancy considerations.
- Biomedical Engineering: Medical implants and devices that operate in bodily fluids rely on controlled buoyancy.
Worked Example 1: Concrete Block Underwater
Scenario:
A reinforced concrete block with a volume of 0.25 m³ is lowered into a freshwater reservoir. Its density is 2400 kg/m³. Determine its effective submerged weight and explain the practical implications for handling.
Step-by-step reasoning:
- The block is heavy in air, over 5800 N.
- When fully submerged, the water displaces about 250 kg of fluid, creating a buoyant force close to 2450 N.
- The submerged weight is therefore reduced to roughly 3350 N.
Engineering implications:
- Cranes or lifting devices must be rated for the submerged weight, not the dry weight, to optimize capacity.
- If the same block were in seawater, the submerged weight would drop further, making handling slightly easier.
- For subsea foundations, this reduction must be accounted for in stability design against uplift or overturning.
Worked Example 2: Subsea Pipeline Buoyancy
Scenario:
An offshore pipeline section, made of steel with external concrete coating, has an outer volume of 1.5 m³ per meter length and a steel-concrete combined density of 3000 kg/m³. The pipeline is placed on the seabed in seawater (density 1025 kg/m³).
Step-by-step reasoning:
- The dry weight per meter exceeds 44 kN.
- The seawater exerts a buoyant force of over 15 kN per meter.
- The submerged weight is therefore about 29 kN per meter.
Engineering implications:
- The reduced effective weight makes the pipeline susceptible to hydrodynamic forces from waves and currents.
- Stabilization techniques, such as rock dumping, trenching, or using heavier coatings, are applied.
- Regulatory frameworks such as DNVGL-ST-F101 explicitly require submerged weight checks during design.
Additional Considerations in Professional Practice
- Temperature and Salinity: Both significantly alter water density, especially in oceanographic contexts. Cold, saline water increases density, reducing submerged weight further.
- Dynamic Effects: Rapid immersion or oscillation can introduce hydrodynamic added mass, which modifies the effective buoyancy in transient states.
- Safety Factors: Standards often require design safety margins to ensure stability, even with density uncertainties.
- Material Porosity: Concrete, timber, and composites may absorb water, altering both true and apparent weights over time.