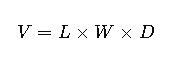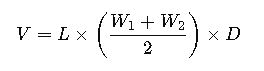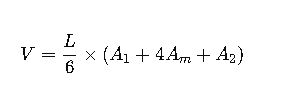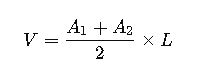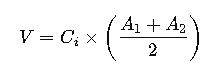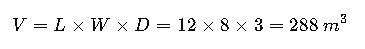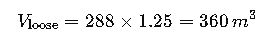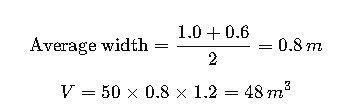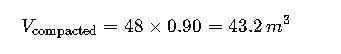Earthwork calculations, especially excavation and backfill volume estimation, are crucial for construction accuracy, cost control, and compliance.
This guide offers formulas, variable explanations, examples, and tables, enabling precise excavation and backfill calculation understanding.
Excavation / Backfill Volume Calculator
Importance of Accurate Volume Calculation
Inaccurate volume estimation can result in:
- Cost overruns due to excess material handling or shortages.
- Schedule delays from unexpected material quantities.
- Design non-compliance with slopes, drainage, or structural requirements.
- Environmental issues such as erosion or improper spoil disposal.
Therefore, precise calculations are essential for both technical performance and financial sustainability of a project.
Common Methods for Volume Calculation
The calculation of excavation or backfill volume depends on the type of excavation, available topographical data, and the shape of the work area. The main methods include:
- Rectangular or Cuboidal Calculation – For regular-shaped excavations.
- Prismoidal Method – For irregular shapes between two cross-sections.
- Average End Area Method – Common in roadway and trench works.
- Contour Method – For large-scale grading projects using topographic maps.
- Digital Terrain Models (DTM) – Using software such as AutoCAD Civil 3D or Trimble Business Center.
Comprehensive Tables of Common Excavation and Backfill Volumes
Below is a reference table of typical excavation shapes with standard dimensions and calculated volumes. These are commonly encountered in foundations, trenches, and basements.
Table 1 – Common Volumes for Rectangular Excavations
| Length (m) | Width (m) | Depth (m) | Volume (m³) |
|---|---|---|---|
| 2.0 | 1.0 | 1.0 | 2.0 |
| 3.0 | 1.5 | 1.2 | 5.4 |
| 4.0 | 2.0 | 1.5 | 12.0 |
| 5.0 | 2.0 | 2.0 | 20.0 |
| 6.0 | 2.5 | 1.8 | 27.0 |
| 8.0 | 3.0 | 2.0 | 48.0 |
| 10.0 | 3.5 | 2.5 | 87.5 |
| 12.0 | 4.0 | 3.0 | 144.0 |
Table 2 – Typical Trench Volumes (Average Width × Depth × Length)
| Length (m) | Average Width (m) | Depth (m) | Volume (m³) |
|---|---|---|---|
| 5.0 | 0.5 | 1.0 | 2.5 |
| 10.0 | 0.6 | 1.2 | 7.2 |
| 15.0 | 0.8 | 1.5 | 18.0 |
| 20.0 | 1.0 | 1.8 | 36.0 |
| 25.0 | 1.2 | 2.0 | 60.0 |
| 30.0 | 1.5 | 2.5 | 112.5 |
Table 3 – Typical Backfill Volumes for Foundations
| Foundation Perimeter (m) | Width of Backfill (m) | Depth (m) | Volume (m³) |
|---|---|---|---|
| 20 | 0.5 | 1.0 | 10.0 |
| 30 | 0.6 | 1.2 | 21.6 |
| 40 | 0.7 | 1.5 | 42.0 |
| 50 | 0.8 | 1.8 | 72.0 |
| 60 | 1.0 | 2.0 | 120.0 |
These values are for quick estimation purposes. For precise calculations, detailed site measurements and design specifications must be applied.
Key Formulas for Excavation and Backfill Volume
The formulas below cover the most common scenarios in excavation and backfill works.
1. Rectangular or Box Excavation
Where:
- V= Volume (m³)
- L= Length of excavation (m)
- W= Width of excavation (m)
- D= Depth of excavation (m)
Common values:
- Length (L): 2–50 m for typical construction pits.
- Width (W): 1–10 m.
- Depth (D): 0.5–5 m.
2. Trench Volume (Average Width Method)
Where:
- W1 = Top width (m)
- W2= Bottom width (m)
- Other variables as above.
3. Prismoidal Formula
Where:
- A1= Area of first cross-section (m²)
- A2= Area of second cross-section (m²)
- Am= Area of mid-section (m²)
- L= Distance between cross-sections (m)
4. Average End Area Method
Used in road construction, drainage canals, and long excavation stretches.
5. Volume from Contour Maps
Using contour intervals:
Where Ci is contour interval height (m).
Real-World Example 1 – Excavation for a Basement
Project: Basement excavation for a residential building.
Given:
- Length = 12 m
- Width = 8 m
- Depth = 3 m
Calculation:
If soil swell factor = 25% (loose volume after excavation):
Real-World Example 2 – Roadside Drainage Trench
Given:
- Length = 50 m
- Top width = 1.0 m
- Bottom width = 0.6 m
- Depth = 1.2 m
Calculation:
If backfilling with compacted soil (compaction factor = 90%):
How do slopes affect excavation volume?
Slopes increase the top width of the excavation, which increases the average width and total volume. Slope ratios depend on soil type and safety codes, e.g., 1.5:1 for loose sand.
What is the swell factor in excavation?
The swell factor accounts for volume increase when soil is excavated and becomes loose. For example, clay may swell 20–30%, meaning 100 m³ in place becomes 120–130 m³ loose.
Why is moisture content important in backfill?
Moisture affects soil density, compaction efficiency, and weight. Optimum Moisture Content (OMC) ensures proper compaction without causing instability or erosion.
Which software is used for excavation volume calculation?
Popular tools include AutoCAD Civil 3D, Trimble Business Center, Topcon MAGNET, and drone photogrammetry software like Agisoft Metashape.
How do you calculate excavation for irregular terrain?
For uneven ground, divide the site into sections, calculate each volume separately using the average end area or contour method, then sum all sections.
What is the difference between bank volume, loose volume, and compacted volume?
- Bank Volume (BCY) – Material in natural, undisturbed state.
- Loose Volume (LCY) – Material after excavation, before compaction.
- Compacted Volume (CCY) – Material after being placed and compacted.
Is GPS surveying accurate for volume measurement?
Yes, modern RTK GPS and total stations can achieve ±2 cm accuracy for volume computations, especially when integrated with DTM-based software.