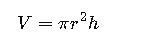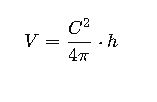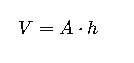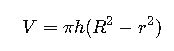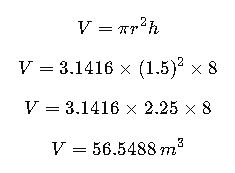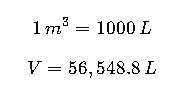Cylinders are essential three-dimensional shapes in engineering, manufacturing, construction, and industrial design, enabling diverse applications.
Accurate volume calculation supports fluid mechanics, materials estimation, and various engineering tasks, ensuring efficiency, precision, and cost-effectiveness.
Calculation of the Volume of a Cylinder
Understanding the Geometry of a Cylinder
A cylinder is a three-dimensional solid with two parallel circular bases connected by a curved surface at a fixed distance (height) from each other.
Key geometric parameters:
- Radius (r): Distance from the center of the circular base to its edge.
- Diameter (d): Distance across the circular base, passing through its center.
Relation: d=2r - Height (h): Perpendicular distance between the two circular bases.
- Volume (V): Space occupied inside the cylinder, usually expressed in cubic units.
Fundamental Formula for the Volume of a Cylinder
The most widely used formula is:
Where:
- V= Volume of the cylinder (in cubic meters, cubic centimeters, liters, etc.)
- π= Pi, a mathematical constant (~3.14159265)
- r= Radius of the base (in meters, centimeters, etc.)
- h= Height of the cylinder (in meters, centimeters, etc.)
Alternative Formula Using Diameter
Since ![]() the formula can also be expressed as: V=π(d2)2hV = \pi \left(\frac{d}{2}\right)^2 hV=π(2d)2h
the formula can also be expressed as: V=π(d2)2hV = \pi \left(\frac{d}{2}\right)^2 hV=π(2d)2h
Where:
- d= Diameter of the cylinder’s base.
This form is especially useful when the diameter is known but the radius is not directly measured.
Engineering Considerations for Variables
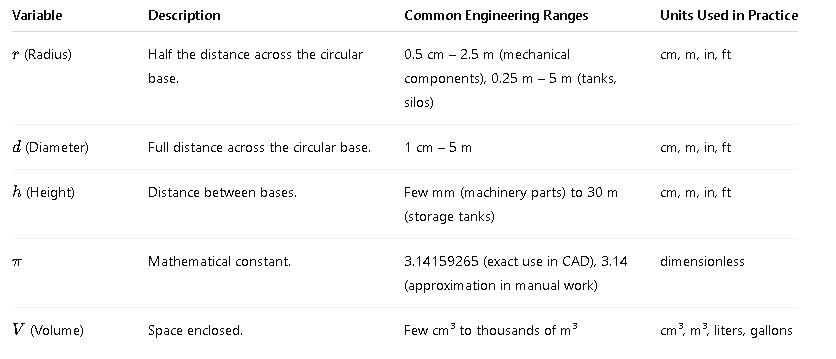
Extended Formula Variations
For some specialized engineering situations, volume calculation can incorporate different measurements:
- Using Circumference (C) of the base:
Where C=2πr.
- Using cross-sectional area (A):
Where A=πr2
- Hollow Cylinders (Tube Volume):
Where:
- R= Outer radius
- r= Inner radius
Extensive Table of Common Cylinder Volumes
Below is a highly detailed reference table for quick engineering and construction estimations.
Values are given in liters (L) and cubic meters (m³), assuming standard π=3.1416\pi = 3.1416π=3.1416.
| Diameter (m) | Radius (m) | Height (m) | Volume (m³) | Volume (L) |
|---|---|---|---|---|
| 0.10 | 0.05 | 0.50 | 0.00393 | 3.93 |
| 0.10 | 0.05 | 1.00 | 0.00785 | 7.85 |
| 0.25 | 0.125 | 1.00 | 0.04909 | 49.09 |
| 0.50 | 0.25 | 1.00 | 0.19635 | 196.35 |
| 0.50 | 0.25 | 2.00 | 0.39270 | 392.70 |
| 1.00 | 0.50 | 1.00 | 0.78540 | 785.40 |
| 1.00 | 0.50 | 2.00 | 1.57080 | 1,570.80 |
| 1.50 | 0.75 | 2.00 | 3.53429 | 3,534.29 |
| 2.00 | 1.00 | 2.00 | 6.28320 | 6,283.20 |
| 2.00 | 1.00 | 5.00 | 15.70796 | 15,707.96 |
| 3.00 | 1.50 | 5.00 | 35.34292 | 35,342.92 |
| 3.00 | 1.50 | 10.00 | 70.68583 | 70,685.83 |
| 4.00 | 2.00 | 5.00 | 62.83200 | 62,832.00 |
| 4.00 | 2.00 | 10.00 | 125.66371 | 125,663.71 |
| 5.00 | 2.50 | 10.00 | 196.34954 | 196,349.54 |
| 6.00 | 3.00 | 10.00 | 282.74334 | 282,743.34 |
This table can be expanded even further to include gallons, cubic feet, and other engineering units if you need a multi-unit reference.
Real-World Application Examples of Cylinder Volume Calculation
Case Study 1: Calculating Water Capacity for an Industrial Storage Tank
Problem Statement:
A food processing plant requires a cylindrical vertical tank to store potable water.
- Diameter = 3.0 m
- Height = 8.0 m
Determine:
- Volume in cubic meters (m³)
- Volume in liters (L)
- Volume in US gallons (gal)
Step-by-Step Solution:
1.Convert given values into variables:
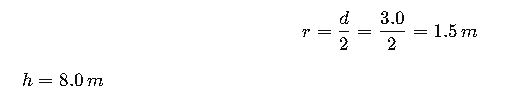
2.Apply the formula:
3.Convert to liters:
4.Convert to US gallons:
Final Answer:
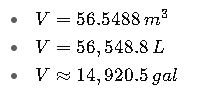
Engineering Note:
When sizing tanks for food processing, it’s essential to account for freeboard (empty space at the top) to prevent overflow during filling. In this case, a 5% freeboard would reduce usable capacity to about 53.72 m³.
Case Study 2: Volume of a Concrete Column for Structural Load Estimation
Problem Statement:
An engineer needs to estimate the volume of concrete required for a cylindrical support column in a parking structure.
- Diameter = 0.6 m
- Height = 4.2 m
Calculate:
- Volume in cubic meters (m³)
- Weight of concrete (assuming density = 2400 kg/m³)
Step-by-Step Solution:

Final Answer:
- V=1.188m3
- Mass ≈ 2.85 metric tons
Engineering Note:
In construction, always round up material volumes to account for waste, spillage, and over-excavation. A 10% contingency would mean ordering 1.31 m³ of concrete.
Extended Multi-Unit Cylinder Volume Table
This table includes m³, liters, US gallons, and cubic feet to make it universally applicable.
| Diameter (m) | Radius (m) | Height (m) | Volume (m³) | Liters (L) | US gal | Cubic ft |
|---|---|---|---|---|---|---|
| 0.10 | 0.05 | 0.50 | 0.00393 | 3.93 | 1.04 | 0.14 |
| 0.25 | 0.125 | 1.00 | 0.04909 | 49.09 | 12.97 | 1.73 |
| 0.50 | 0.25 | 1.00 | 0.19635 | 196.35 | 51.87 | 6.93 |
| 1.00 | 0.50 | 2.00 | 1.57080 | 1,570.80 | 414.94 | 55.48 |
| 1.50 | 0.75 | 2.00 | 3.53429 | 3,534.29 | 933.94 | 124.80 |
| 2.00 | 1.00 | 5.00 | 15.70796 | 15,707.96 | 4,147.99 | 554.48 |
| 3.00 | 1.50 | 5.00 | 35.34292 | 35,342.92 | 9,328.49 | 1,246.54 |
| 4.00 | 2.00 | 10.00 | 125.66371 | 125,663.71 | 33,021.90 | 4,436.88 |
| 5.00 | 2.50 | 10.00 | 196.34954 | 196,349.54 | 51,709.25 | 6,957.75 |
| 6.00 | 3.00 | 10.00 | 282.74334 | 282,743.34 | 74,257.69 | 9,905.26 |
Conversions Used:
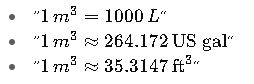
Practical Notes for Engineers and Designers
- Measurement Accuracy – Small errors in radius measurement can lead to large volume errors because radius is squared in the formula.
- Material Expansion – In fluids, temperature changes can cause expansion; capacity calculations should consider operating temperature.
- Manufacturing Tolerances – Cylindrical components in precision machining require tighter dimensional control compared to large concrete or steel structures.
- Standards and References – For pressure vessels and tanks, refer to ASME Boiler & Pressure Vessel Code (ASME Standards).
- Fluid Storage Design – For chemical storage, consult API 650 for welded tanks (API Standards).