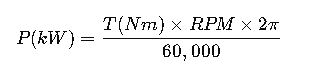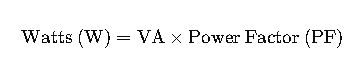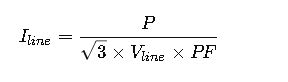A powerful guide on short-circuit current calculation in generators lights up safe, efficient design improvements and reliable analyses. This article deciphers essential formulas, variables, and methods step-by-step.
Detailed insights on short-circuit current calculation methods – both with and without the exciter – empower engineers to optimize protection design, improve system reliability, and ensure compliance with industry standards.
AI-powered calculator for Calculation of short-circuit current in generators with and without exciter
Example Prompts
- Calculate short-circuit current for a 10 MVA generator with a 0.2 p.u. excitation factor.
- Determine I_sc for a 15 MVA generator without excitation using a 5% reactance.
- Compute fault current for a 20 MVA generator with an exciter in a 50 Hz system at 11 kV.
- Find short-circuit current for a 12 MVA generator with given terminal impedance and exciter resistance.
Fundamental Concepts of Short-Circuit Current in Generators
1. When fault conditions occur, a generator delivers a surge current that can be expressed in relation to available internal energy and impedance.
The short-circuit current calculation is driven by the generator’s internal EMF, stator impedance, and, where applicable, the contribution of the exciter system. This understanding is crucial for proper circuit breaker sizing and protection element coordination.
Elements Influencing Short-Circuit Current
1. The generator’s rating (MVA and voltage levels).
The internal impedance, including both resistance and reactance elements, plays a vital role in determining the magnitude of the short-circuit current during fault situations.
1. The network’s configuration and interconnection impact.
Interconnections with system reactances, transformer impedances, and the contribution of the exciter through its influence on internal EMF, are important analysis factors.
The Role of Exciters in Generator Performance
1. Exciters supply the necessary DC current to produce a magnetic field in the generator’s rotor, defining the internal electromotive force (EMF).
Without an exciter, generators generally rely on residual magnetism and may behave differently during faults, affecting the calculated short-circuit current magnitude. With an exciter, the generator’s voltage regulation characteristics alter the effective impedance seen during faults.
1. Exciter-controlled generators provide dynamic responses through automatic voltage regulators (AVR) which optimize short-circuit current based on load or fault detection.
This dynamic control not only contributes to the transient fault current magnitude but can also influence the transient stability of the system, resulting in upgraded protection coordination strategies.
Essential Formulas for Calculating Short-Circuit Current
1. A common formula for calculating short-circuit current (I_sc) in generators is given by:
1. Where:
- E represents the generator’s internal electromotive force (EMF) in volts.
- Z_total is the total impedance in ohms, which sums the generator’s internal impedance along with line and transformer impedances.
In systems equipped with an exciter, the effective EMF (E_eff) is often higher due to the controlled excitation current, implying that the short-circuit current calculation is influenced by the excitation level.
1. In generators without an exciter, or where the exciter is not operational, the residual magnetism defines a lower EMF value leading to a modified formula:
1. Here, the variables are defined as:
- k is a factor representing the residual excitation, typically in the range of 0.1 to 0.3 for many designs.
- V_rated is the rated generator voltage.
Understanding these variables and relationships is essential for high-fidelity modeling and allows for accurate fault current predictions during system design and fault studies.
Expanding the Calculation: Additional Considerations
1. Apart from internal generator parameters, consider aspects such as sub-transient, transient, and steady-state reactances for comprehensive analysis.
The sub-transient reactance (X”d) is especially relevant immediately after a fault occurs. Analyses of the sub-transient current provide insights into the initial inrush and determine the short-circuit magnitude before stabilization.
1. The detailed formula incorporating sub-transient reactance (X” d) is:
1. Here:
- R is the resistance component of the generator’s impedance.
- X”d is the sub-transient reactance which is lower relative to transient or synchronous reactance values.
This formula emphasizes the immediate peak fault currents experienced during transient fault conditions, which are critical in designing protection apparatus such as fuses and circuit breakers.
1. The contribution of the exciter in steady-state operation may yield a recalculated steady-state short-circuit current as:
1. Here:
- E_eff is the effective internal EMF adjusted by the AVR and exciter system.
- Z_total comprises internal impedance plus extrinsic impedances from connected systems.
This distinction between initial and steady-state conditions helps engineers design protective devices that must react appropriately to both short impulses and sustained fault currents.
Comparative Table: Generator Parameters and Short-Circuit Calculations
| Parameter | With Exciter | Without Exciter |
|---|---|---|
| Internal EMF (E) | Controlled by AVR; Higher value | Dependent on residual magnetism; Lower value |
| Short-Circuit Current (I_sc) | Calculated using effective EMF; Typically higher | Calculated using residual excitation factor (k) |
| Impedance (Z_total) | Internal + external impedances considered | Same impedance, but different effective voltage |
| Excitation Factor | Active and adaptive | Passive; relies on residual magnetism |
Detailed Real-Life Application Examples
Example 1: Calculation Without an Exciter
1. Consider a generator with a rated voltage of 11 kV and a rated power of 10 MVA. The generator shows a residual excitation with a factor k = 0.2. The total impedance Z_total is determined to be 0.5 ohms.
For this generator, the effective EMF is computed as: E_effective = k × V_rated. Thus, E_effective = 0.2 × 11,000 V = 2,200 V. Using the basic formula, the short-circuit current is: I_sc = E_effective / Z_total = 2,200 / 0.5 = 4,400 A.
1. To further refine the calculation, consider the scenario where the generator’s resistance is R = 0.1 ohm and its sub-transient reactance X”d = 0.4 ohm. The initial short-circuit current becomes:
1. Substituting the known values gives:
R² = (0.1)² = 0.01 ohm² and (X”d)² = (0.4)² = 0.16 ohm², so √(0.01 + 0.16) = √0.17 ≈ 0.412 ohms. Thus, I_sc_initial ≈ 2,200 V / 0.412 ohms ≈ 5,340 A.
1. This example demonstrates that without an active exciter, inherent design limitations lower the effective EMF, yet fault conditions result in significant fault currents due to low impedance paths.
Engineers use these calculations for designing relay settings and ensuring that protective devices, like circuit breakers, are appropriately rated for fault clearing capability.
Example 2: Calculation With an Exciter
1. Now, consider a 15 MVA generator operating at a rated voltage of 11 kV, equipped with an automatic voltage regulator (AVR) and exciter system. Due to regulation, the effective internal EMF is slightly enhanced to approximately 1.05 times the rated value under fault conditions. Hence:
Effective internal EMF E_eff = 1.05 × 11,000 V = 11,550 V. Assume the total impedance Z_total (including generator and network contributions) is measured at 1.2 ohm. The short-circuit current calculation becomes: I_sc = E_eff / Z_total = 11,550 / 1.2 ≈ 9,625 A.
1. For a more detailed evaluation immediately after the fault, with R = 0.15 ohm and X”d = 0.7 ohm, the expression transforms to:
1. Evaluate R² = (0.15)² = 0.0225 ohm² and (X”d)² = (0.7)² = 0.49 ohm², yielding:
√(0.0225 + 0.49)= √0.5125 ≈ 0.716 ohms, so I_sc_initial ≈ 11,550 V / 0.716 ohms ≈ 16,141 A.
1. This example emphasizes that, with an active exciter, the generator can develop a higher effective EMF, thereby leading to increased fault currents which are managed by advanced protection coordination schemes.
The calculation reinforces the need for periodic testing and accurate parameter determination to ensure protective relays and circuit breakers respond reliably during short-circuit events.
Additional Practical Considerations in Fault Analysis
1. In-line network impedances and transformer contributions must be included.
Often, the total impedance seen by a fault is not just that of the generator. In connected power systems, line and transformer impedances, as well as contributions from parallel generation sources, cause variations in the computed fault currents.
1. The transient and dynamic behavior of faults necessitates the inclusion of time-based parameters.
Detailed transient stability studies require the use of time-domain simulation software to capture the rapidly changing short-circuit currents, particularly in systems with complex excitation control systems.
1. The impact of temperature and frequency must be accounted for, as these factors affect both resistance and reactance.
For systems operating at non-nominal frequencies or in extreme temperature conditions, the impedance values may deviate from nominal values, introducing further complexity into short-circuit current calculations.
Expanding the Analysis with Software Tools and Simulation
1. Several industry-standard software platforms facilitate detailed and dynamic short-circuit analysis.
Software tools such as ETAP, power system simulation packages, and custom utilities integrated into control system software allow engineers to simulate fault conditions and accurately model generator and network behaviors.
1. Integration of simulation results with hardware-in-the-loop (HIL) testing provides a robust validation mechanism for protection schemes.
Such testing setups replicate fault conditions in real time, validating the calculated short-circuit currents and ensuring that protective devices operate as expected under transient overload conditions.
1. Modern digital fault recorders can capture transient behaviors, allowing for empirical validation and model refinement.
Empirical data from fault recorders and oscilloscope traces further enable the adjustment of models to account for the nuances introduced by the exciter, confirming the calculated values with real-world performance measurements.
Understanding the Impact of Sub-Transient Reactance
1. Sub-transient reactance (X”d) provides a snapshot of the generator’s initial reactance immediately after a fault, typically governing the peak short-circuit current.
X”d is extremely relevant for the design of protective devices, as the immediate fault current can exceed steady-state values dramatically, demanding fast-acting interruption devices.
1. The calculation method employing X”d, as shown previously, quickly determines the initial current surge that protective relays must accommodate.
Engineering standards such as IEEE C37 and IEC 60909 recommend the use of sub-transient reactance values for initial fault current estimations in design studies.
1. In many generator models, the sub-transient reactance is about 30–50% of the synchronous reactance, providing a basis for comparative analysis among different generator designs.
This parameter becomes especially critical during generator testing and commissioning activities to ensure that transient protection coordination aligns with predicted fault current levels.
Tables of Typical Generator Impedance Values
| Generator Type | Sub-Transient Reactance (X”d) [p.u.] | Synchronous Reactance [p.u.] | Typical Residual Excitation Factor (k) |
|---|---|---|---|
| Hydroelectric Generator | 0.20 – 0.30 | 1.00 – 1.20 | 0.15 – 0.25 |
| Thermal Generator | 0.25 – 0.35 | 0.90 – 1.10 | 0.10 – 0.20 |
| Wind Turbine Generator | 0.30 – 0.40 | 1.10 – 1.30 | 0.05 – 0.15 |
| Diesel Generator | 0.35 – 0.50 | 1.20 – 1.40 | 0.10 – 0.30 |
Best Practices for Accurate Short-Circuit Calculations
1. Ensure thorough measurement and verification of all generator parameters, including rated voltage, MVA, impedance, and excitation control settings.
Accurate data acquisition during commissioning, periodic maintenance, and testing substantially reduces uncertainties in fault current predictions.
1. Regular calibration of testing instruments and the use of updated simulation models help ensure that computed short-circuit currents reflect actual operating conditions.
Modern digital fault recorders, high-speed sampling devices, and integrated simulation software packages facilitate ongoing validation against actual fault events, enhancing confidence in calculated values.
1. Adhere to international standards and guidelines such as IEEE C37 series, IEC 60909, and regional electrical regulations when performing short-circuit current calculations.
These standards provide robust frameworks for defining the parameters, methodologies, and safety margins essential in designing protection schemes that can safely interrupt fault currents.
Frequently Asked Questions
- What is the significance of the excitation factor (k) in calculations?
The excitation factor determines the portion of the rated voltage available when the exciter is not operating. It adjusts the generator’s effective EMF, thus impacting the short-circuit current magnitude.
- Why do short-circuit currents differ between generators with and without exciters?
The exciter influences the internal EMF; a generator with an active exciter may produce a higher effective EMF (and therefore higher short-circuit current) compared to one operating under residual magnetism alone.
- How are network impedances integrated into the total impedance (Z_total) calculation?
Z_total includes the generator’s internal impedance alongside external factors such as the impedance of lines, transformers, and switching equipment, crucial in determining the actual fault current.
- What roles do sub-transient and synchronous reactances play in transient fault analysis?
Sub-transient reactance (X”d) defines the peak initial fault current, while synchronous reactance is more indicative of the steady-state current magnitude after the immediate transient period.
- How can engineers use simulation tools for improved fault current calculations?
Simulation tools allow for precise modeling of fault dynamics, incorporating real-time factors such as excitation control and network impedance. These tools support designing better protection schemes by replicating transient and steady-state conditions.
Integration with Modern Electrical Systems and Safety Protocols
1. Incorporating short-circuit current calculations into plant design improves safety protocols and helps in selecting appropriate protective devices.
Smart grid approaches rely on real-time current monitoring and adaptive protection schemes that benefit from robust short-circuit current modeling and simulation data.
1. The integration of wide-area monitoring systems (WAMS) allows for more accurate real-time fault detection and validation of calculated values.
Data from phasor measurement units (PMUs) complement calculated fault currents by giving immediate insights into system response, enabling predictive maintenance and dynamic load management.
1. Regular training and updates on new modeling techniques and simulation tools help keep engineering teams abreast of the latest developments in fault analysis.
Continual education ensures that protection schematics, relay settings, and circuit breaker ratings are maintained in line with the most recent electrical standards and improved calculation methods.
Advanced Topics in Generator Protection Coordination
1. Modern protection schemes integrate algorithms that continuously update fault current estimates during transient events, blending historical data with live measurements.
Such adaptive protection not only offers improved resilience against faults but also aids system operators in initiating preemptive measures to isolate and mitigate electrical faults.
1. The inclusion of distributed generation and renewable energy sources further complicates short-circuit calculations, requiring integrated studies to consider bidirectional power flows.
Engineers must account for varied generation profiles, interfacing multiple technologies with differing excitation systems to accurately predict fault currents across the network.
1. Coordination between generation, transmission, and distribution protection devices is paramount.
By utilizing centralized system studies and simulation models, overall system reliability is enhanced while minimizing the risk of cascading failures during fault events.
Ensuring Compliance with Electrical Regulations and Best Practices
1. All calculations must adhere to international certifications and local regulations that guide short-circuit and safety analysis.
Regulatory frameworks such as those defined by IEEE, IEC, and regional authorities dictate acceptable calculation methods, safety margins, and periodic testing requirements to protect both assets and personnel.
1. Documentation of all calculation steps, parameters used, and simulation outcomes must be maintained for auditing and compliance reviews.
Accurate record-keeping allows for continuous improvement of protective systems, ensuring that any modifications to system configuration or operating conditions are duly analyzed and validated.
Summary of Steps for Short-Circuit Current Calculation
- Identify generator ratings, including voltage (V_rated) and power (MVA).
- Determine the available excitation level:
- For generators with exciter: measure effective internal EMF (E_eff) adjusted by the AVR.
- For generators without exciter: apply the residual excitation factor (k).
- Calculate total impedance (Z_total) incorporating internal generator impedance and external components (lines, transformers).
- For initial fault current, use sub-transient reactance (X”d) and resistance (R) to compute I_sc_initial.
- For steady-state analysis, use effective EMF (E or E_eff) divided by Z_total to obtain I_sc.
Carefully following these steps ensures accurate short-circuit current predictions, improves protection device coordination, and enhances safety across generation and distribution networks.
Real-World Impacts on System Design and Reliability
1. The calculation of short-circuit currents is critical not only for device coordination in power systems but also for understanding the impact of switching transients during emergency isolation.
Through proper short-circuit analysis, system designers can foresee potential overloads, ensuring that circuit breakers and protective relays do not unintentionally trip during transient events, maintaining system stability under fault conditions.
1. Efficient management of short-circuit conditions can reduce equipment stress, thereby extending the lifetime of both generators and network components.
By designing systems that accurately accommodate high fault currents, unnecessary maintenance costs are minimized and overall reliability is improved, crediting the advances in excitation control and dynamic protection schemes.
Leveraging Authoritative External Resources
1. For additional theoretical and practical insights, consider visiting reputable sources such as:
IEEE – Institute of Electrical and Electronics Engineers and IEC – International Electrotechnical Commission.
1. These organizations provide in-depth technical standards, case studies, and ongoing research updates that enhance understanding of generator protection and fault current analysis.
Professional bodies and conferences regularly discuss improvements in measurement techniques, simulation software, and new adaptive control strategies which can be invaluable for improved engineering practices.
Embracing Future Trends in Generator Fault Analysis
1. Advances in digital instrumentation, artificial intelligence, and machine learning are redefining how fault current calculations are integrated into smart grid management.
Future systems will be capable of real-time predictive fault analysis, continuously optimizing generator parameters and dynamically adjusting protection schemes for enhanced operational resilience.
1. Continued research into fault dynamics, excitation control algorithms, and transient analysis tools will further refine calculation accuracy and protective device coordination.
As renewable integration grows and grid complexity increases, the need for precise, adaptive fault management becomes ever more critical, transforming short-circuit current estimation into a cornerstone of modern electrical engineering.
1. Industry-wide collaboration and knowledge sharing will further enhance methodologies, ensuring that short-circuit calculations keep pace with emerging technologies and evolving grid architectures.
By leveraging advanced simulation capabilities and integrating empirical data from smart monitoring systems, future power systems will achieve unprecedented reliability and safety margins during both planned and unplanned fault conditions.
Final Thoughts on Calculation of Short-Circuit Currents
1. Accurate determination of short-circuit currents—whether using generators equipped with exciters or operating solely on residual magnetism—is a vital component of power system safety and equipment design.
The detailed methodologies, formulas, and real-world examples provided empower engineers to design robust, compliant, and efficient systems that withstand fault conditions and minimize downtime.
1. Embracing both theoretical and practical approaches, including simulation tools and field data, ensures that engineers are well-equipped to tackle the complexities of modern power systems.
This comprehensive article serves as an essential resource for anyone involved in power system design, protection coordination, and system analysis, offering clear insights and actionable guidance on short-circuit current calculations.