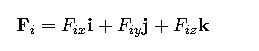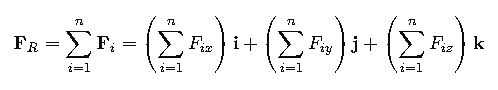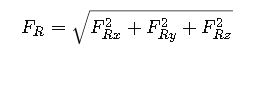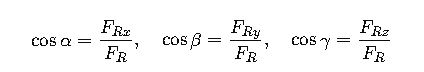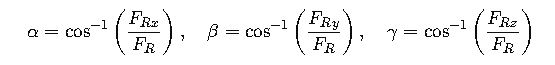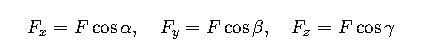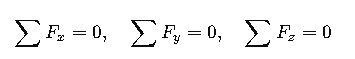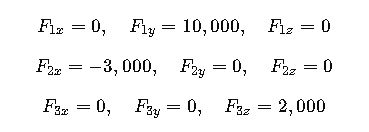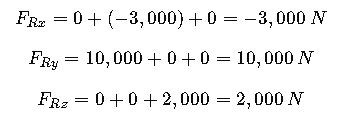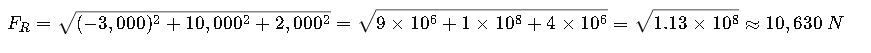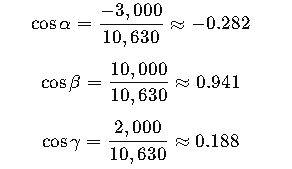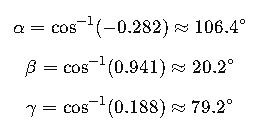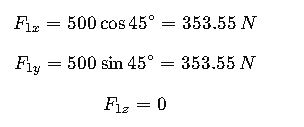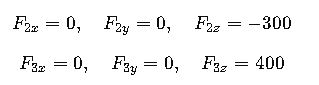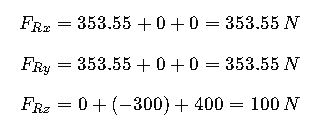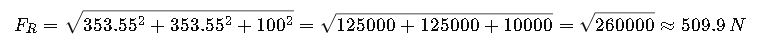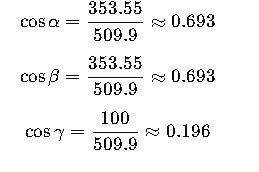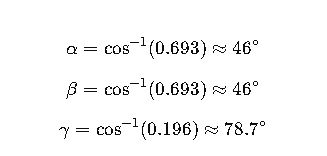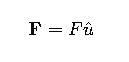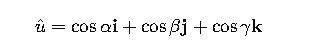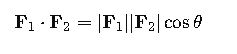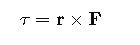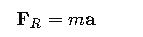Calculation of Resultant Force in Three Dimensions

Understanding resultant force in three dimensions is essential for accurate analysis in engineering and physics. It enables designing stable structures, analyzing mechanical systems, and controlling forces in robotics and aerospace.

Accurate calculation ensures safety, reliability, and efficiency across various applications, including civil engineering and dynamic systems. Mastery of these principles is fundamental for professional engineers and physicists.

Resultant Force Calculator (3D)

Force X (N): Force Y (N): Force Z (N):

Extensive Table of Common Values for Resultant Force Components and Angles

This table summarizes typical force components (in Newtons) and angles (degrees) often encountered in engineering problems involving three-dimensional forces.

Force Component (N)	Fx (N)	Fy (N)	Fz (N)	Magnitude F (N)	Direction Cosines (cos α, cos β, cos γ)	Angles (α, β, γ in degrees)
Example 1	50	75	100	134.54	0.372, 0.559, 0.743	68.2°, 56.0°, 42.1°
Example 2	120	160	80	213.29	0.562, 0.75, 0.375	55.7°, 41.4°, 67.9°
Example 3	0	100	100	141.42	0, 0.707, 0.707	90°, 45°, 45°
Example 4	30	40	0	50	0.6, 0.8, 0	53.13°, 36.87°, 90°
Example 5	10	10	10	17.32	0.577, 0.577, 0.577	54.7°, 54.7°, 54.7°

Fundamental Formulas for Calculation of Resultant Force in Three Dimensions

1. Resultant Force Vector

Given multiple forces F₁, F₂, …, Fₙ, each with components along the x, y, and z axes:

The resultant force FR is the vector sum:

Where:

Fix,Fiy,Fiz are the force components along the x, y, and z axes for the i-th force.

2. Magnitude of the Resultant Force

The magnitude FR of the resultant force vector FR is computed using the Euclidean norm:

Where:

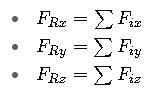
3. Direction Cosines and Angles of Resultant Force

The direction cosines cos⁡α, cos⁡β, and cos⁡γ describe the orientation of the resultant force vector relative to the coordinate axes:

The angles α,β,γ\alpha, \beta, \gammaα,β,γ between the force vector and the coordinate axes are:

4. Component Calculation from Magnitude and Angles

Sometimes forces are given by magnitude and direction angles instead of components:

5. Equilibrium Condition in 3D

For a system in static equilibrium:

Each sum represents the algebraic sum of force components in the respective axis direction.

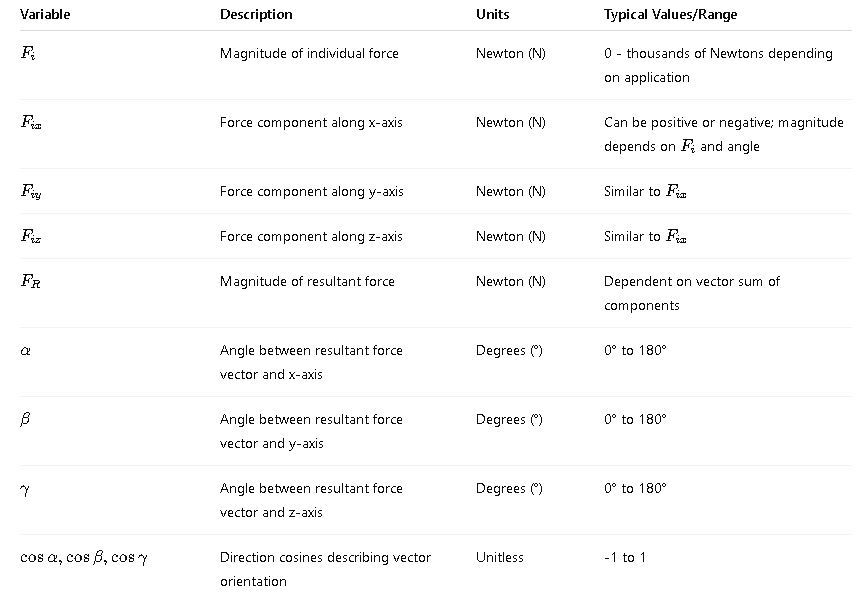
Explanation of Variables and Common Values

Real-World Examples of Resultant Force in Three Dimensions

Example 1: Aerospace – Calculating the Resultant Force on an Aircraft Wing

Scenario:
An aircraft wing experiences three forces due to aerodynamic pressure, gravity, and thrust vectoring.

F1 (lift force): 10,000 N acting upward along the y-axis.
F2 (drag force): 3,000 N acting backward along the x-axis (negative x direction).
F3 (side wind): 2,000 N acting perpendicular to the wing span along the z-axis.

Step 1: Define components

Step 2: Calculate resultant components

Step 3: Calculate magnitude

Step 4: Calculate direction cosines

Step 5: Calculate angles

Interpretation:
The resultant force has a magnitude of ~10.63 kN, directed mostly upwards along y-axis with a backward and slight sideways component.

Example 2: Civil Engineering – Forces on a Structural Joint

Scenario:
A joint in a truss structure is subjected to three forces:

F1: 500 N along a 45° angle from the x-axis toward the y-axis in the xy-plane (z=0).
F2: 300 N acting straight down (negative z-axis).
F3: 400 N acting along the z-axis upward.

Step 1: Resolve F1 into components

Since F1 lies in the xy-plane at 45°: