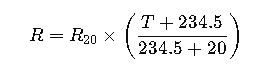Mixing two solutions with different temperatures is a common problem in engineering that involves energy balance and specific heat calculations.
In this article, you will find detailed formulas, tables, practical examples, and expert FAQs on calculating mixtures with precision.
AI-powered calculator for Calculation of Mixtures of Two Solutions with Different Temperatures
Example Prompts
- Mix 50 L at 60°C with 30 L at 20°C
- Combine 100 kg at 80°C with 150 kg at 30°C
- Calculate 20 L at 75°C with 25 L at 40°C
- Determine final temperature for 80 kg at 90°C and 120 kg at 10°C
Understanding the Calculation of Mixtures of Two Solutions with Different Temperatures
The calculation of mixtures with different temperatures largely relies on the principle of energy conservation and the assumption of no heat loss. The energy gained by one solution equals the energy lost by the other during mixing.
In practical applications, engineers use this calculation to predict the final temperature after mixing. It helps in minimizing risks and optimizing industrial processes such as chemical reactions and heating systems.
This process is governed by the fundamental equation of heat balance. It states that the total heat content before mixing must equal the total heat content after mixing, provided that the system is isolated from any heat exchange with the surroundings.
For mixtures where both solutions have similar heat capacities, the common formula combines masses and their respective temperatures into one equation. This mathematical principle is essential in thermal dynamics and process engineering.
Key Variables and Their Meanings
Before diving into the formulas, it is essential to understand the variables used in these calculations. Engineers generally deal with the following parameters:
- m₁ and m₂: Masses (or volumes, when densities are equal) of the two solutions.
- T₁ and T₂: Initial temperatures of the two solutions measured in °C or Kelvin.
- Tₑ: The equilibrium or final temperature after mixing.
- c: Specific heat capacity of the solution, representing the energy required to raise the temperature of one unit mass by one degree Celsius (for water, typically 4.18 J/g°C).
Often in engineering, when a substance’s density and specific heat capacity are constant, the value of c can be omitted from the calculations (as it cancels out). However, if two different liquids are mixed, it is imperative to include the specific heat capacities of both.
Fundamental Formula for Temperature Calculation
The primary formula for calculating the final temperature when two solutions mix without heat loss is derived from the conservation of energy:
For clarity:
- m₁: Mass (or volume) of the first solution
- m₂: Mass (or volume) of the second solution
- T₁: Temperature of the first solution
- T₂: Temperature of the second solution
- Tₑ: The resulting equilibrium temperature after mixing
This equation assumes that both solutions have uniform properties and that the specific heat capacity remains constant.
When the two solutions possess different specific heat capacities, the formula adapts by incorporating each solution’s c-value:
Here:
- c₁: Specific heat capacity of the first solution
- c₂: Specific heat capacity of the second solution
This variation is particularly useful in chemical engineering when combining substances with very different thermal properties.
Extended Considerations
In addition to the core energy balance, engineers must also consider:
- The possibility of phase changes, particularly if the temperatures approach the boiling point or melting point.
- Total volume change, since mixing solutions might result in contraction or expansion.
- Heat losses to the environment, which is critical in non-ideal, real-world applications. If losses are significant, more detailed thermodynamic models are employed.
These factors, although secondary in simple calculations, become critical in high-precision engineering applications such as chemical reactor design or thermal management in large-scale processes.
Extensive Table of Variables and Their Parameters
| Parameter | Symbol | Unit | Description |
|---|---|---|---|
| Mass / Volume (Solution 1) | m₁ | kg / L | Represents the quantity of the first solution |
| Mass / Volume (Solution 2) | m₂ | kg / L | Represents the quantity of the second solution |
| Initial Temperature (Solution 1) | T₁ | °C / K | Initial temperature of solution one |
| Initial Temperature (Solution 2) | T₂ | °C / K | Initial temperature of solution two |
| Specific Heat Capacity (Solution 1) | c₁ | J/g°C | The energy required to raise the temperature of solution one |
| Specific Heat Capacity (Solution 2) | c₂ | J/g°C | The energy required to raise the temperature of solution two |
| Final Equilibrium Temperature | Tₑ | °C / K | The temperature after the solutions are mixed |
This table helps engineers quickly reference the variables and their respective units when preparing calculations for mixtures with different temperatures.
When dealing with multi-component systems or more complex industrial processes, similar tables are created to account for additional parameters such as density variations, volumetric thermal expansion, and other thermophysical properties.
Engineering Applications and Case Studies
Real-life applications of the mixture of two solutions with different temperatures are prevalent in everyday life and industry alike. These instances demonstrate the importance of precise calculations in ensuring safety and optimization.
The following sections detail two real-world case studies with thorough calculations, showcasing how these principles are applied in practical scenarios.
Case Study 1: Household Water Heating System
Consider a simple household scenario where a plumber mixes hot water and cold water to achieve a comfortable bathing temperature. In this example, a homeowner wishes to combine 50 liters of water at 60°C with 30 liters at 20°C.
Step 1: Identify the variables. Here:
- m₁ = 50 L (hot water)
- T₁ = 60°C
- m₂ = 30 L (cold water)
- T₂ = 20°C
Step 2: Since water has a uniform specific heat capacity and assuming no heat losses, use the energy balance equation:
Calculating:
- Energy contributed by hot water = 50 × 60 = 3000
- Energy contributed by cold water = 30 × 20 = 600
- Total energy = 3000 + 600 = 3600
- Total volume = 50 + 30 = 80
Thus, Tₑ = 3600 / 80 = 45°C. The resulting mixture is at a comfortable temperature suitable for bathing.
This example demonstrates a straightforward application of the energy conservation principle in a domestic water heating system. Furthermore, it shows the importance of proper calculations to avoid scalding and ensure safety.
Case Study 2: Industrial Chemical Reactor Temperature Control
In industrial applications, precise temperature control is critical to ensure optimally performing chemical reactions. Consider a scenario where an industrial process requires mixing two chemical solutions at different temperatures to reach a reaction temperature of 70°C. Here, the involved solutions have different specific heat capacities.
Process Details:
- Solution A: 100 kg at 90°C with a specific heat capacity (c₁) = 3.5 J/g°C
- Solution B: 150 kg at 40°C with a specific heat capacity (c₂) = 4.0 J/g°C
Step 1: Convert masses to grams if needed: 100 kg = 100,000 g and 150 kg = 150,000 g. However, if both masses are in the same unit, they cancel out if we maintain consistency. For our purpose, we use kg and adjust the specific heat capacities accordingly (assuming consistency in unit conversion):
Step 2: Use the enhanced formula:
Substitute the values:
- m₁ = 100 kg, T₁ = 90°C, c₁ = 3.5 J/g°C (or 3500 J/kg°C)
- m₂ = 150 kg, T₂ = 40°C, c₂ = 4.0 J/g°C (or 4000 J/kg°C)
Step 3: Calculate the numerator:
- Energy from A = 100 × 3500 × 90 = 31,500,000 J
- Energy from B = 150 × 4000 × 40 = 24,000,000 J
- Total energy = 31,500,000 + 24,000,000 = 55,500,000 J
Step 4: Calculate the denominator:
- Total heat capacity = 100 × 3500 + 150 × 4000 = 350,000 + 600,000 = 950,000 J/°C
Thus, Tₑ = 55,500,000 J / 950,000 J/°C ≈ 58.42°C. Although the target was 70°C, the calculations indicate that the current masses and temperatures will not reach the desired reaction temperature. Adjustments in the proportions or initial temperatures must be made.
This example not only emphasizes the importance of correct thermal calculations in safety-critical industrial environments but also reveals how slight variations in specific heat capacities can affect the final outcome markedly.
Advanced Topics in Temperature Mixing Calculations
Beyond the basic calculations, several advanced topics deserve attention. Understanding these can improve process control and design in more sophisticated applications.
One advanced consideration is when the mixing process involves chemical reactions. Exothermic or endothermic reactions could alter the heat balance significantly. In such cases, the energy balance equation should include the reaction enthalpy (ΔH) as an additional term. The modified formula is expressed as:
Where Q_reaction represents the net heat generated or absorbed during the chemical reaction. This term must be carefully measured or calculated for each specific reaction.
Another advanced topic is the inclusion of a heat loss parameter, especially when the mixing container is not perfectly insulated. The general energy balance will then account for the environmental heat exchange term:
Here, Q_loss is typically estimated based on the container’s insulation characteristics and ambient temperature. Proper assessment of Q_loss is imperative in high-precision applications such as cryogenics and high-temperature industrial processes.
Furthermore, simulation software and numerical methods often extend these formulations to dynamically control mixing processes. For instance, computational fluid dynamics (CFD) tools can simulate the heat transfer in mixing tanks, providing insights into achieving uniform temperature distribution during mixing.
These advanced techniques are critical for optimizing large-scale industrial operations and ensuring both quality control and operational safety.
Guidelines for Implementing Calculations in the Field
When applying these calculations on-site, several practical guidelines need to be followed:
- Accuracy: Always use accurately measured quantities and calibrated instruments to measure temperature and mass/volume.
- Safety: Consider safety margins, especially when mixing substances with significantly different temperatures.
- Insulation: Account for possible heat loss or gain during mixing by ensuring proper insulation of the mixing vessel.
- Software Tools: Utilize engineering software and AI-powered calculators for more complex scenarios, especially in industrial settings.
- Expert Consultation: For processes involving hazardous materials, consult with experienced engineers and safety experts.
Following these guidelines ensures that the temperature mixing process is executed with both accuracy and safety, reducing the risk of equipment failure or hazardous incidents.
In addition, maintaining detailed records of each mixing process can help in troubleshooting and refining the procedure. It is common practice in high-stakes industries to develop standard operating procedures (SOPs) that incorporate detailed calculation methods and constant monitoring.
Comparison with Alternative Approaches
While the energy balance method described here is the most widely used, some alternative approaches exist. Among these alternatives is the use of iterative methods and simulation-based approaches to refine the mixing temperature predictions.
For example, some processes utilize sensor networks installed in industrial reactors to monitor temperature gradients continuously. Instead of relying solely on static calculations, real-time data is combined with predictive modeling to adjust input parameters. These adaptive techniques ensure that the final mixture consistently meets the desired temperature specifications.
Another method involves employing phase diagram analyses, especially in cases where component interactions are complex. In such systems, the mixing process may involve temperature-dependent solubility and conductivity changes, which must be accounted for. This holistic approach often involves both empirical testing and theoretical calculations.
However, for the majority of engineering applications where the properties of the solutions are well-defined, the direct energy balance remains the most efficient and reliable method. The simplicity of the formula ensures rapid decision-making and minimal computational overhead, making it ideal for both small-scale operations and real-time industrial processes.
Frequently Asked Questions (FAQs)
Q1: When is extra care required when calculating the final temperature of mixtures?
A: Extra care is required when solutions have significantly different specific heat capacities, when phase changes may occur, or when reactions release/absorb heat. Always consider possible heat losses.
Q2: Can I use the same calculations if the solutions are of different substances?
A: Yes, but ensure to use the correct specific heat capacities (c₁ and c₂) for each substance. Not factoring these differences may lead to inaccurate temperature predictions.
Q3: What should I do if I have additional heat exchange with the environment?
A: Include an extra term in your energy balance equation to account for Q_loss or Q_gain from the surroundings. Insulated conditions are ideal for basic calculations.
Q4: How accurate are these calculations in real-world industrial applications?
A: They are highly accurate provided that all parameters, such as mass, temperature, and specific heat capacities, are measured correctly. Environmental losses and reaction enthalpies must be accounted for in more complex systems.
Q5: Are there software tools to assist with these calculations?
A: Yes, various engineering simulation software, including CFD tools, and AI-powered calculators are available to enhance accuracy and provide real-time feedback for industrial processes. For further reading on simulation techniques, check resources like Engineering Toolbox and Computational Fluid Dynamics on Wikipedia.
Implementing Calculation Techniques in Software
Modern engineering processes often integrate these calculations into custom software solutions or use specialized applications for real-time monitoring. The incorporation of these equations into control systems can significantly enhance process automation by providing near-instantaneous temperature predictions for mixed solutions.
Developers can implement these formulas in programming languages such as Python, MATLAB, or C++, which allow the integration of sensors and data acquisition modules. For example, a simple Python algorithm may involve input parameters such as:
- mass1, mass2
- temp1, temp2
- specific heat values
The script then computes the final temperature using the aforementioned formulas, and outputs the result through a GUI dashboard or an industrial control panel.
This implementation not only provides error-free calculations but also allows for extensive logging, thereby facilitating troubleshooting and refinement of the process over time. AI-powered calculators, as showcased at the beginning of this article, further simplify these calculations by incorporating machine learning algorithms to predict outcomes even when some input parameters may vary.
Moreover, integrating these systems with IoT (Internet of Things) networks further enhances automation and reliability by enabling remote monitoring and control. This is particularly beneficial in large industrial plants where manual monitoring is impractical.
Best Practices in Engineering Calculations for Mixed Temperature Solutions
When using these calculations in practice, adhere to the following best practices:
- Calibration: Regularly calibrate measurement instruments to ensure accurate input data for the calculations.
- Documentation: Maintain comprehensive documentation for all calculations. This ensures traceability and facilitates any required audits.
- Redundancy: Cross-check calculations using multiple independent methods or software to minimize errors.
- Training: Ensure that all staff handling the mixing process are well-trained in both the theoretical background and practical aspects of these calculations.
- Continuous Improvement: Update calculation methods and software regularly to incorporate advances in science and technology, maintaining compliance with current industry standards.
Establishing these best practices can significantly enhance both safety and efficiency. The use of example calculations, like those provided herein, serves as a template for evaluating system performance and guiding future process optimizations.
In addition, quality control measures, such as statistical process control (SPC), can further enhance reliability by monitoring deviations over time, ensuring that the processes remain within acceptable limits.
Additional Resources and Further Reading
For engineers and practitioners seeking more detailed discussions on the principles of thermal mixing and energy conservation, the following authoritative links are recommended:
- American Society of Mechanical Engineers (ASME)
- Indian Institute of Technology Kanpur – Research Papers on Thermal Processes
- ScienceDirect – Journals on Heat Transfer and Thermodynamics
- National Institute of Standards and Technology (NIST) – Data on Thermophysical Properties
These resources provide deeper insights and practical guidance on thermodynamic processes, ensuring that users stay updated on the latest advancements in thermal calculations and process optimization.
Engaging with academic articles, industry white papers, and technical workshops can further reinforce the understanding of complex mixing phenomena.
Summary of Key Concepts
In summary, the calculation of mixtures with different temperatures is a fundamental concept in thermal engineering, adopting principles from basic energy conservation. By using established formulas, engineers can determine the final equilibrium temperature effectively.
Understanding and applying the energy balance equations along with the specific attributes of each solution—such as mass, temperature, and specific heat capacity—ensures accurate predictions for varied process conditions. From household water heating to industrial chemical reactions, the same underlying principles govern the outcomes.
Moreover, embracing advanced topics such as reaction enthalpy inclusion, real-time sensors, and simulation-based corrections enhance the reliability and efficiency of the temperature mixing process. Utilizing automated software and adhering to best practices helps minimize errors and improve operational safety.
With these techniques and guidelines in hand, engineers are well-equipped to design robust systems that accomplish precise temperature mixing, ultimately contributing to more efficient and safer industrial processes.
Further Exploration
For those interested in deepening their expertise, consider exploring research articles and case studies that examine the thermodynamics of fluid mixing in greater detail. Whether you are working in process engineering, chemical manufacturing, or HVAC design, continued education in these principles can drive innovation and quality improvements in your projects.
Over time, as experimental data is collected and simulation models are refined, the predictive accuracy of these calculations will continue to improve, offering engineers new insights for optimizing energy usage and reducing operational costs.
Remember, the key to successful temperature calculation in mixing scenarios lies in a systematic approach: measure accurately, calculate correctly, and validate thoroughly. This article has laid out the foundational principles, provided detailed formulas and practical examples, and highlighted best practices essential for mastering these calculations.
By following these guidelines and leveraging modern computational tools, you can confidently tackle even the most challenging temperature mixing problems, ensuring both innovation and safety in your engineering endeavors.