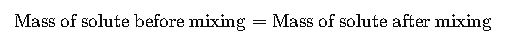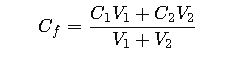The calculation of mixtures with different concentrations is fundamental in chemistry, engineering, food, and pharmaceuticals. Accurate mixture calculations guarantee reproducibility, safety, and compliance when combining solutions across laboratory and industrial environments.
Mixture Calculator — Two Solutions
Calculate resulting concentration or the required volume of one solution to reach a target concentration. Works with % w/v, % v/v or any consistent unit.
How does the math work?
Which units are allowed?
Examples / formulas used
Solve for V₂: V₂ = (Cₓ·Vₓ – C₁·V₁) / (C₂ – Cₓ), with Vₓ = desired final volume (V₁+V₂) or computed accordingly.
Solve for V₁ similar by swapping indexes.
Importance of Mixture Calculations
Mixtures of two solutions are frequently used in:
- Pharmaceutical production: Dilution of active pharmaceutical ingredients (APIs) to therapeutic concentrations.
- Clinical laboratories: Preparing calibration standards or adjusting reagent concentrations.
- Food industry: Adjusting sugar, salt, or acid concentrations in beverages or canned products.
- Water treatment: Mixing disinfectants or chemicals for achieving target residual concentrations.
- Chemical manufacturing: Achieving specific molarities for synthesis or analysis.
Failing to calculate properly can lead to unsafe products, ineffective treatments, or process failures.
Core Formulas for Mixture Calculations
When two solutions with different concentrations are mixed, the concentration of the final mixture depends on the masses of solute contributed by each solution and the total volume.
The general balance equation is:

This formula is derived from the principle of mass balance:
Explanation of Variables
- Concentration (C): Expressed in different units depending on context:
- Molarity (mol/L)
- Mass percent (%)
- Weight/Volume percentage (w/v %)
- Parts per million (ppm) or parts per billion (ppb)
- Volume (V): Usually measured in liters (L) or milliliters (mL).
- Final concentration (Cf): The concentration of the combined solution, determined by weighted contribution of solutes.
Extended Formula Set for Different Scenarios

Extensive Tables of Common Mixture Calculations
To provide a quick reference, the following tables present common calculations for mixing two solutions of varying concentrations. These are built for clarity and practical use in laboratories.
Table 1. Mixing Equal Volumes of Two Solutions (V₁ = V₂)
| C₁ (%) | C₂ (%) | V₁ (mL) | V₂ (mL) | Cᶠ (%) | Notes |
|---|---|---|---|---|---|
| 10 | 0 | 100 | 100 | 5.0 | Simple dilution by half |
| 20 | 10 | 100 | 100 | 15.0 | Average concentration |
| 30 | 10 | 100 | 100 | 20.0 | Used in reagent prep |
| 50 | 0 | 100 | 100 | 25.0 | Dilution with pure solvent |
| 80 | 40 | 100 | 100 | 60.0 | Midpoint concentration |
Table 2. Unequal Volumes (V₁ ≠ V₂)
| C₁ (%) | V₁ (mL) | C₂ (%) | V₂ (mL) | Cᶠ (%) |
|---|---|---|---|---|
| 10 | 100 | 0 | 50 | 6.7 |
| 20 | 200 | 5 | 100 | 15.0 |
| 50 | 50 | 10 | 150 | 20.0 |
| 80 | 30 | 40 | 70 | 52.0 |
| 90 | 10 | 0 | 90 | 9.0 |
Table 3. Molarity Calculations (Mixing mol/L solutions)
| C₁ (mol/L) | V₁ (mL) | C₂ (mol/L) | V₂ (mL) | Cᶠ (mol/L) |
|---|---|---|---|---|
| 1.0 | 100 | 0.0 | 100 | 0.50 |
| 0.5 | 200 | 0.2 | 100 | 0.40 |
| 2.0 | 50 | 1.0 | 50 | 1.50 |
| 3.0 | 100 | 0.5 | 300 | 1.125 |
| 5.0 | 25 | 1.0 | 75 | 2.00 |
Table 4. Dilution with Solvent (C₂ = 0)
| Initial Concentration (%) | V₁ (mL) | Added Solvent V₂ (mL) | Final Concentration (%) |
|---|---|---|---|
| 10 | 100 | 100 | 5.0 |
| 20 | 50 | 150 | 5.0 |
| 15 | 200 | 50 | 12.0 |
| 25 | 40 | 60 | 10.0 |
| 5 | 500 | 500 | 2.5 |
Step-by-Step Explanation of Formula Application
1.Identify initial concentrations (C₁ and C₂).
- For chemical reagents, this may be given as molarity or percent solution.
2.Determine the volumes to be mixed (V₁ and V₂).
- Typically measured with volumetric flasks or pipettes.
3.Apply the general formula.
- Insert known values into the equation:
4.Check units.
- Ensure that concentrations are expressed in consistent units.
5.Perform calculation and verify plausibility.
- The result should lie between the lower and higher concentration.
Real-World Application Example 1: Pharmaceutical Preparation
Problem:
A pharmacist needs to prepare 250 mL of a 15% solution of ethanol by mixing available stock solutions of 10% and 20%.
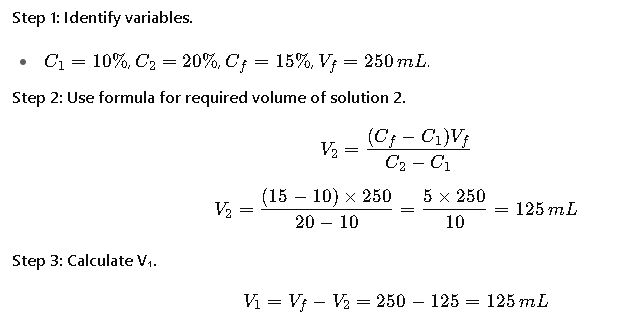
Result:
Mix 125 mL of 10% ethanol with 125 mL of 20% ethanol to obtain 250 mL of 15%.
Industry Relevance:
This is a routine calculation in hospital pharmacies when compounding personalized medications.
Real-World Application Example 2: Water Treatment
Problem:
A municipal water plant needs to prepare 1,000 L of chlorine solution at 3 mg/L concentration. They have available stocks at 5 mg/L and 1 mg/L.
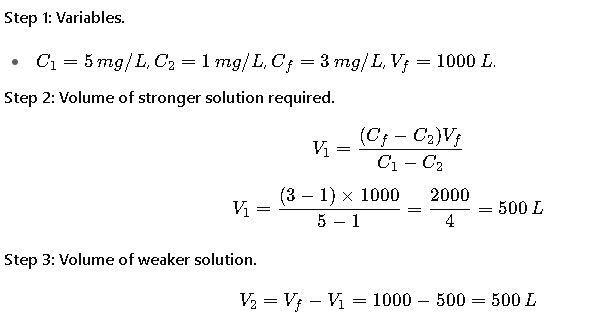
Result:
Mix 500 L of 5 mg/L chlorine with 500 L of 1 mg/L chlorine to obtain 1,000 L of 3 mg/L solution.
Industry Relevance:
This method ensures regulatory compliance with U.S. EPA Drinking Water Standards.
Practical Applications Across Industries
The calculation of mixtures of two solutions with different concentrations is not confined to academic exercises. It is an essential practice in industrial and laboratory settings where precision directly impacts safety, compliance, and quality control.
Pharmaceutical Industry
- Drug compounding: Hospital pharmacies frequently mix active ingredients of different concentrations to achieve individualized dosages.
- Sterile preparations: Intravenous solutions often require combining concentrated stock solutions with diluents to reach therapeutic levels.
- Regulatory compliance: Authorities such as the U.S. Food and Drug Administration and the European Medicines Agency require strict adherence to defined concentration ranges.
Water Treatment and Environmental Engineering
- Chlorination: Plants mix chlorine solutions of different concentrations to ensure adequate disinfection.
- Fluoridation: Adjustment of fluoride levels in municipal water supplies often involves combining solutions of varying strengths.
- Wastewater management: Treatment facilities balance acidic and alkaline solutions to maintain pH within safe limits.
Food and Beverage Industry
- Juice concentration: Producers mix concentrated syrups with water to achieve consistent sugar content.
- Salt solutions: Food processors adjust salinity levels when brining or curing products.
- Acid balance: In beverage formulation, acids like citric or lactic acid are mixed to achieve target acidity and flavor.
Chemical and Biochemical Laboratories
- Buffer preparation: Biochemists often mix stock solutions to create buffers at exact molarities for experiments.
- Nutrient media: Microbiologists mix growth media solutions with additives of varying concentrations to maintain reproducibility.
- Analytical chemistry: Calibration standards for spectroscopy or chromatography are prepared by mixing solutions with different analyte concentrations.
Extended Reference Tables
To make the process more intuitive, here are additional tables that illustrate common scenarios encountered in laboratories and industry.
Table 5. Mixtures at Laboratory Scale (milliliters, percentage concentration)
| Solution 1 (%) | Volume (mL) | Solution 2 (%) | Volume (mL) | Final (%) |
|---|---|---|---|---|
| 2 | 50 | 8 | 50 | 5.0 |
| 4 | 30 | 12 | 70 | 10.4 |
| 5 | 200 | 20 | 100 | 10.0 |
| 15 | 150 | 5 | 50 | 12.5 |
| 25 | 100 | 0 | 100 | 12.5 |
Table 6. Mixtures at Industrial Scale (liters, ppm values)
| Solution 1 (ppm) | Volume (L) | Solution 2 (ppm) | Volume (L) | Final (ppm) |
|---|---|---|---|---|
| 100 | 500 | 0 | 500 | 50 |
| 200 | 1000 | 50 | 1000 | 125 |
| 300 | 200 | 100 | 800 | 140 |
| 500 | 100 | 250 | 900 | 275 |
| 1000 | 50 | 100 | 950 | 145 |
Table 7. Food Industry Common Mixtures (grams of solute per liter)
| Syrup 1 (g/L sugar) | Volume (L) | Syrup 2 (g/L sugar) | Volume (L) | Final (g/L sugar) |
|---|---|---|---|---|
| 50 | 10 | 200 | 10 | 125 |
| 100 | 5 | 300 | 15 | 250 |
| 150 | 20 | 0 | 20 | 75 |
| 80 | 12 | 120 | 8 | 96 |
| 250 | 30 | 100 | 10 | 212.5 |
Additional Real-World Scenarios
Case Study 3: Biochemistry – Buffer Preparation
A research lab requires a phosphate buffer of intermediate strength. Instead of preparing it from scratch, two stock solutions of differing molarities are mixed. By calculating the appropriate ratios, the lab ensures reproducibility across experiments, reducing variability in enzyme activity studies.
Case Study 4: Beverage Production – Sugar Adjustment
A beverage manufacturer prepares a fruit drink where sweetness must remain consistent. Available syrups are at 100 g/L and 200 g/L sugar concentrations. By mixing exact volumes, the company ensures every production batch tastes the same, avoiding customer complaints and meeting food labeling requirements.
Best Practices in Mixture Calculations
- Maintain unit consistency
- Always use the same system (liters with liters, molarity with molarity).
- Account for temperature and density
- Concentrations can change slightly with temperature, especially in industrial processes.
- Use calibrated equipment
- Pipettes, flasks, and tanks must be calibrated to avoid volume errors.
- Verify with analytical testing
- In pharmaceuticals and food industries, laboratory confirmation (e.g., titration, spectroscopy) is mandatory.
- Apply safety margins
- Particularly in toxic or hazardous chemical preparations, small errors can have significant consequences.
Common Mistakes and How to Avoid Them
- Mixing incompatible units: For example, combining percentages with molarities without conversion.
- Ignoring solvent effects: In some cases, volumes are not perfectly additive (e.g., ethanol and water).
- Overlooking stock purity: Assumed concentrations may differ from actual values due to degradation or impurities.
- Failing to validate: Relying solely on theoretical calculation without experimental confirmation can lead to dangerous errors.
Optimization for Industrial Workflows
- Batch scaling: Automated systems in chemical plants use programmable logic controllers (PLCs) to calculate mixture ratios dynamically.
- Digital calculators: Many industries implement web-based or embedded calculators for mixture concentration adjustments.
- Regulatory compliance: Standards such as ISO 17025 emphasize documentation and traceability of calculations in laboratories.
- Automation and AI integration: Advanced facilities now use predictive algorithms to adjust mixing ratios in real time based on sensor feedback.
Frequently Asked Questions (FAQs)
1. Why is calculating mixtures with two solutions important?
Because precision in concentration determines the effectiveness, safety, and regulatory compliance of laboratory and industrial processes.
2. Can mixture calculations be applied beyond chemistry?
Yes. Similar principles are used in agriculture (fertilizer mixing), medicine (intravenous solutions), and even in beverage recipes.
3. Are the calculations the same for ppm, percent, and molarity?
Yes, the principle is the same, but units must remain consistent throughout the calculation.
4. What happens if volumes are not additive?
In cases like mixing ethanol with water, total volume may contract. Experimental correction is required.
5. Which standards regulate mixture calculations?
Pharmaceutical industries follow FDA and EMA guidelines, water treatment follows EPA and WHO standards, and food industries align with Codex Alimentarius.