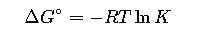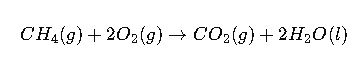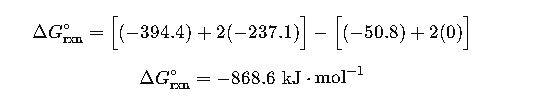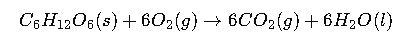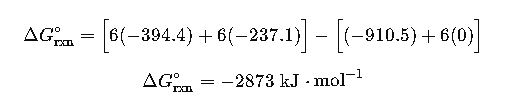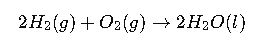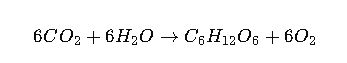The Gibbs free energy change (ΔG) is a thermodynamic property predicting chemical or physical process spontaneity. It integrates enthalpy, entropy, and temperature, providing criteria for reaction feasibility under constant pressure and temperature.
Gibbs Free Energy (ΔG) Calculator
Compute ΔG = ΔH − T·ΔS with unit handling (J ↔ kJ, °C ↔ K). Enter ΔH and ΔS with units, set temperature, and get ΔG in J/mol and kJ/mol plus spontaneity and equilibrium temperature.
Fundamental Concept of Gibbs Free Energy
The Gibbs free energy GGG is defined as:
G=H−TS
Where:
- H= Enthalpy (kJ·mol⁻¹), representing total heat content.
- T= Absolute temperature (Kelvin, K).
- S = Entropy (J·mol⁻¹·K⁻¹), representing the degree of disorder.
The change in Gibbs free energy during a process is expressed as:

This simple criterion makes Gibbs free energy indispensable in chemistry, biochemistry, materials science, and engineering.
Extensive Reference Tables for Gibbs Free Energy Calculations
The following tables summarize standard Gibbs free energy of formation (ΔGf∘) values for common substances at 298 K (25 °C). These are widely used in calculations.
Table 1: Common Standard Gibbs Free Energy of Formation Values
| Substance | Formula | ΔGf° (kJ·mol⁻¹) | Phase |
|---|---|---|---|
| Hydrogen gas | H₂ | 0.0 | g |
| Oxygen gas | O₂ | 0.0 | g |
| Nitrogen gas | N₂ | 0.0 | g |
| Carbon dioxide | CO₂ | -394.4 | g |
| Carbon monoxide | CO | -137.2 | g |
| Methane | CH₄ | -50.8 | g |
| Ethane | C₂H₆ | -32.9 | g |
| Ammonia | NH₃ | -16.5 | g |
| Nitric oxide | NO | +86.6 | g |
| Nitrogen dioxide | NO₂ | +51.3 | g |
| Water (liquid) | H₂O | -237.1 | l |
| Water (gas) | H₂O | -228.6 | g |
| Sulfur dioxide | SO₂ | -300.4 | g |
| Sulfur trioxide | SO₃ | -370.4 | g |
| Hydrochloric acid | HCl | -95.3 | g |
| Sodium hydroxide (solid) | NaOH | -379.5 | s |
| Glucose | C₆H₁₂O₆ | -910.5 | s |
Notes:
- Elements in their standard states (H₂, O₂, N₂, etc.) always have ΔGf° = 0.
- Negative values indicate that formation is thermodynamically favorable under standard conditions.
Key Formulas for Calculating Gibbs Free Energy
There are several essential formulas used in ΔG calculations, depending on the system and conditions.
1. Direct Thermodynamic Definition
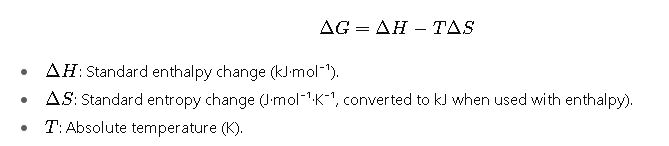
This is the core formula in thermodynamics.
2. Using Standard Gibbs Free Energies of Formation
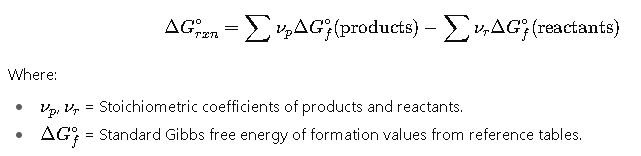
This is the most common method for practical chemical calculations.
3. Relation with the Equilibrium Constant
Where:
- R= Gas constant = 8.314 J·mol⁻¹·K⁻¹.
- T= Temperature in Kelvin.
- K= Equilibrium constant.
This equation establishes the bridge between thermodynamics and equilibrium chemistry.
4. Non-Standard Conditions
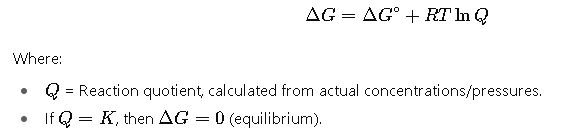
This formula is crucial in predicting whether a reaction mixture will proceed forward or backward.
Common Ranges of Thermodynamic Variables
For accuracy, it is useful to know typical ranges of values:
Table 2: Typical Values of Thermodynamic Parameters
| Variable | Range (Common) | Units | Notes |
|---|---|---|---|
| ΔH | -1000 to +1000 | kJ·mol⁻¹ | Large negative: highly exothermic. |
| ΔS | -200 to +400 | J·mol⁻¹·K⁻¹ | Positive values: increased disorder. |
| ΔG | -500 to +500 | kJ·mol⁻¹ | Negative values indicate spontaneity. |
| T | 200 – 2000 | K | Standard lab = 298 K. |
Real-World Applications of Gibbs Free Energy Calculations
Case Study 1: Combustion of Methane
Reaction:
Step 1: Collect ΔGf° values (kJ·mol⁻¹):
- CH₄ (g): -50.8
- O₂ (g): 0
- CO₂ (g): -394.4
- H₂O (l): -237.1
Step 2: Apply formula:
Interpretation: The combustion of methane is highly spontaneous, releasing significant free energy, which explains its widespread use as a fuel.
Case Study 2: Metabolism of Glucose (Biological Application)
Reaction (simplified):
Step 1: Collect ΔGf° values:
- Glucose (s): -910.5
- O₂ (g): 0
- CO₂ (g): -394.4
- H₂O (l): -237.1
Step 2: Apply formula:
Interpretation: Cellular respiration releases enormous Gibbs free energy, which is stored in ATP molecules to power biological functions.
Temperature Dependence of Gibbs Free Energy
While the formulas show the theoretical relationship, it is more useful to understand the practical trends. Temperature plays a decisive role in whether a reaction becomes spontaneous.
- Exothermic reactions (ΔH < 0) with increased disorder (ΔS > 0): Almost always spontaneous at all temperatures. Example: combustion reactions.
- Exothermic reactions with decreased disorder (ΔS < 0): Often spontaneous only at low temperatures. Example: condensation of steam into liquid water.
- Endothermic reactions (ΔH > 0) with increased disorder (ΔS > 0): May become spontaneous at higher temperatures. Example: melting of ice above 0 °C.
- Endothermic reactions with decreased disorder: Rarely spontaneous under natural conditions.
Table 3: Reaction Spontaneity Trends
| ΔH Sign | ΔS Sign | Effect of Temperature | Typical Example |
|---|---|---|---|
| Negative | Positive | Always spontaneous | Hydrocarbon combustion |
| Negative | Negative | Spontaneous at low T | Water freezing |
| Positive | Positive | Spontaneous at high T | Ice melting |
| Positive | Negative | Never spontaneous | Non-natural processes |
This classification is widely used in chemical engineering and materials science to predict process feasibility.
Gibbs Free Energy in Electrochemistry
One of the most powerful applications of ΔG is in electrochemical cells. The relationship between Gibbs free energy and electrical work allows us to directly connect thermodynamics with measurable voltages.
The essential principle is:
- A negative ΔG corresponds to a positive cell potential (E°), meaning the cell can generate useful work.
- A positive ΔG corresponds to a negative cell potential, meaning the process requires external energy input (like in electrolysis).
Table 4: Selected Electrochemical Reactions and Gibbs Free Energy
| Reaction (at 298 K) | Cell Potential (E°) | ΔG° (kJ·mol⁻¹) | Application |
|---|---|---|---|
| Zn (s) + Cu²⁺ → Zn²⁺ + Cu (s) | +1.10 V | -212 | Galvanic batteries |
| 2 H₂ + O₂ → 2 H₂O (l) | +1.23 V | -237 | Fuel cells |
| Electrolysis of water (reverse reaction) | -1.23 V | +237 | Hydrogen production |
| Ag⁺ + e⁻ → Ag (s) | +0.80 V | -77 | Silver plating |
These values highlight the connection between electrochemical efficiency and free energy change, a central concept in renewable energy storage.
Industrial and Technological Relevance
The importance of Gibbs free energy is not confined to laboratories; it defines whether large-scale processes are economically and energetically viable.
1. Metal Extraction
Smelting metals from ores is governed by ΔG. For example, the reduction of iron oxide to iron in blast furnaces is only possible because the Gibbs free energy of carbon monoxide reacting with oxygen is more negative than that of iron oxide. Engineers use Ellingham diagrams—plots of ΔG versus temperature—to determine which reducing agents will work at industrial scales.
2. Battery Development
Lithium-ion batteries depend on precise ΔG values for intercalation reactions. A more negative Gibbs free energy means higher cell potential and thus higher energy density. Research in solid-state batteries often focuses on tuning Gibbs free energy landscapes to stabilize ionic transport while maintaining safety.
3. Environmental Engineering
Processes like carbon capture and storage (CCS) must account for Gibbs free energy to evaluate if CO₂ can be absorbed and released efficiently. A negative ΔG ensures that absorption occurs spontaneously, but regeneration (release) often requires energy input, which is a critical economic factor.
Expanded Real-World Example: Hydrogen Fuel Cells
Hydrogen fuel cells convert chemical energy into electricity using the reaction of hydrogen with oxygen:
From a ΔG perspective:
- The standard Gibbs free energy change is approximately -474 kJ·mol⁻¹ (per 2 moles of water formed).
- This translates into a maximum cell potential of about 1.23 V under standard conditions.
In reality, fuel cells operate below this ideal value due to irreversibilities (polarization losses, mass transport issues, and resistive heating). Still, understanding Gibbs free energy allows engineers to calculate the theoretical efficiency ceiling, which for hydrogen fuel cells is close to 83%, significantly higher than combustion engines.
Practical Impact: This is why governments and industries are investing heavily in hydrogen energy: the thermodynamic potential is extremely favorable, and the only by-product is water.
Extended Real-World Example: Photosynthesis
Photosynthesis is an endergonic process (ΔG > 0) that requires an external energy source—sunlight. The simplified reaction is:
- The Gibbs free energy change is approximately +2870 kJ·mol⁻¹.
- This positive value means the reaction cannot occur spontaneously. Instead, solar photons provide the necessary energy input to drive the process.
Relevance:
- Understanding ΔG in photosynthesis helps in the design of artificial photosynthesis systems, a major field of renewable energy research.
- By mimicking nature’s energy conversion, scientists aim to develop efficient solar-to-fuel technologies, turning CO₂ back into useful hydrocarbons.